题目内容
4.不等式sinx≥$\frac{\sqrt{3}}{2}$的解集为{x|2kπ+$\frac{π}{3}$≤x≤2kπ+$\frac{2π}{3}$,k∈Z}.分析 由特殊角的三角函数值和正弦函数的图象可得.
解答 解:∵sin$\frac{2π}{3}$=sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$,∴结合正弦函数的图象可得
不等式sinx≥$\frac{\sqrt{3}}{2}$的解集为{x|2kπ+$\frac{π}{3}$≤x≤2kπ+$\frac{2π}{3}$,k∈Z}
故答案为:{x|2kπ+$\frac{π}{3}$≤x≤2kπ+$\frac{2π}{3}$,k∈Z}
点评 本题考查正弦函数的图象和性质,属基础题.

练习册系列答案
相关题目
20.下列说法中,正确的是( )
| A. | 集合{x|x∈Z,|x|<2}的非空真子集的个数是7 | |
| B. | 函数y=($\frac{1}{2}$)${\;}^{{x}^{2}-3x+2}$的单调递减区间是(-∞,$\frac{3}{2}$] | |
| C. | 已知函数f(x)是定义在R上的奇函数,当x∈(-∞,0)时,f(x)=x-x4,则当x∈(0,+∞)时,f(x)=-x-x4 | |
| D. | 已知f($\frac{2}{x}$+1)=x+3,则f(x)=$\frac{3x-1}{x-1}$ |
14.已知向量$\overrightarrow{a}$=(sinθ,-2)与$\overrightarrow{b}$=(1,cosθ)互相垂直,其中θ∈$(0,\frac{π}{2})$,则sinθ+cosθ等于( )
| A. | $\frac{{-\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{3\sqrt{5}}}{5}$ |
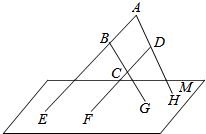 如图,四边形ABCD中,AB∥DC,AB,BC,DC,AD(或其延长线)分别与平面M相交于E,F,G,H,求证:E,F,G,H必在同一直线上.
如图,四边形ABCD中,AB∥DC,AB,BC,DC,AD(或其延长线)分别与平面M相交于E,F,G,H,求证:E,F,G,H必在同一直线上.