题目内容
(本小题满分12分)已知函数 .
.
(Ⅰ)设 ,讨论
,讨论 的单调性;
的单调性;
(Ⅱ)若对任意 恒有
恒有 ,求
,求 的取值范围.
的取值范围.
 .
.(Ⅰ)设
 ,讨论
,讨论 的单调性;
的单调性;(Ⅱ)若对任意
 恒有
恒有 ,求
,求 的取值范围.
的取值范围.解:(1)  的定义域为(
的定义域为( ,1)
,1) (1,
(1, )
)


因为 (其中
(其中 )恒成立,所以
)恒成立,所以 .…………………2分
.…………………2分
当 时,
时, 在(
在( ,0)
,0) (1,
(1, )上恒成立,所以
)上恒成立,所以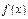 在(
在( ,1)
,1) (1,
(1, )上为增函数; …………………………………4分
)上为增函数; …………………………………4分
当 时,
时, 在(
在( ,0)
,0) (0,1)
(0,1) (1,
(1, )上恒成立,所以
)上恒成立,所以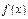 在(
在( ,1)
,1) (1,
(1, )上为增函数;……………………………
)上为增函数;…………………………… ……6分
……6分
当 时,
时, 的解为:(
的解为:( ,
, )
) (t,1)
(t,1) (1,+
(1,+ )
)
(其中 ).
).
所以 在各区间内的增减性如下表:
在各区间内的增减性如下表:
…………………………………8分
(2)显然
(1)当 时,
时, 在区间
在区间 0,1
0,1 上是增函数,所以对任意
上是增函数,所以对任意 (0,1)都有
(0,1)都有 ;
;
(2)当 时,
时, 是
是 在区间
在区间  0,1
0,1 上的最小值,即
上的最小值,即 ,这与题目要求矛盾;
,这与题目要求矛盾;
(3)若 ,
, 在区间
在区间 0,1
0,1 上是增函数,所以对任意
上是增函数,所以对任意 (0,1)都有
(0,1)都有 .
.
综合(1)、(2)、(3) ,a的取值范围为( ,2). …………………………12分
,2). …………………………12分
 的定义域为(
的定义域为( ,1)
,1) (1,
(1, )
)

因为
 (其中
(其中 )恒成立,所以
)恒成立,所以 .…………………2分
.…………………2分当
 时,
时, 在(
在( ,0)
,0) (1,
(1, )上恒成立,所以
)上恒成立,所以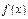 在(
在( ,1)
,1) (1,
(1, )上为增函数; …………………………………4分
)上为增函数; …………………………………4分当
 时,
时, 在(
在( ,0)
,0) (0,1)
(0,1) (1,
(1, )上恒成立,所以
)上恒成立,所以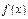 在(
在( ,1)
,1) (1,
(1, )上为增函数;……………………………
)上为增函数;…………………………… ……6分
……6分当
 时,
时, 的解为:(
的解为:( ,
, )
) (t,1)
(t,1) (1,+
(1,+ )
)(其中
 ).
).所以
 在各区间内的增减性如下表:
在各区间内的增减性如下表:| 区间 | ( , , ) ) | ( ,t) ,t) | (t,1) | (1,+ ) ) |
 的符号 的符号 | + |  | + | + |
 的单调性 的单调性 | 增函数 | 减函数 | 增函数 | 增函数 |
(2)显然

(1)当
 时,
时, 在区间
在区间 0,1
0,1 上是增函数,所以对任意
上是增函数,所以对任意 (0,1)都有
(0,1)都有 ;
;(2)当
 时,
时, 是
是 在区间
在区间  0,1
0,1 上的最小值,即
上的最小值,即 ,这与题目要求矛盾;
,这与题目要求矛盾;(3)若
 ,
, 在区间
在区间 0,1
0,1 上是增函数,所以对任意
上是增函数,所以对任意 (0,1)都有
(0,1)都有 .
.综合(1)、(2)、(3) ,a的取值范围为(
 ,2). …………………………12分
,2). …………………………12分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在(0,
在(0, ) 内有极值.
) 内有极值. ).求证:f (x2)-f (x1)>e+2-
).求证:f (x2)-f (x1)>e+2-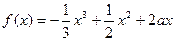 .
.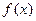 在
在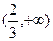 上存在单调递增区间,求
上存在单调递增区间,求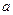 的取值范围;
的取值范围;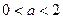 时,
时,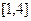 上的最小值为
上的最小值为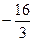 ,求
,求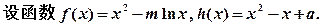
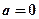 时,
时,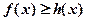 在
在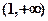 上恒成立,求实数
上恒成立,求实数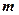 的取值范围;
的取值范围;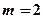 时,若函数
时,若函数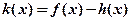 在
在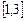 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数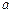 的取值范围;
的取值范围;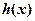 在公共定义域上具有相同的单调区间?若存在,求出
在公共定义域上具有相同的单调区间?若存在,求出 .
. 在区间[-3,4]
在区间[-3,4] 上的值域
上的值域




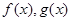 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当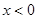 时,
时,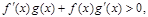 且
且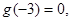 则不等式
则不等式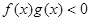 的解集是______________
的解集是______________