题目内容
如图,已知四边形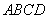 是正方形,
是正方形,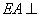 平面
平面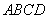 ,
,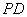
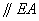 ,
,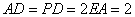 ,
,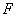 ,
,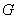 ,
,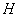 分别为
分别为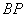 ,
,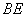 ,
,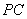 的中点.
的中点.
(Ⅰ)求证: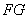
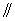 平面
平面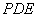 ;
;
(Ⅱ)求证:平面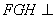 平面
平面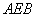 ;
;
(Ⅲ)在线段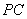 上是否存在一点
上是否存在一点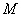 ,使
,使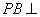 平面
平面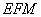 ?
?
若存在,求出线段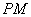 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

 (Ⅰ)证明:因为
(Ⅰ)证明:因为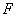 ,
,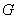 分别为
分别为 ,
,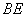 的中点,
的中点,
所以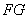
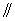
 .
.
又因为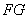
 平面
平面 ,
,
 平面
平面 ,
,
所以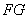
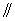 平面
平面 .
.
(Ⅱ)因为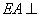 平面
平面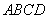 ,所以
,所以 .
.
又因为 ,
, ,
,
所以 平面
平面 .
.
由已知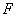 ,
,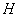 分别为线段
分别为线段 ,
,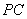 的中点,
的中点,
所以
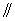
 .
.
则 平面
平面 .
.
而 平面
平面 ,
,
所以平面
 平面
平面 .
.
(Ⅲ)在线段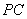 上存在一点
上存在一点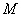 ,使
,使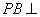 平面
平面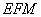 .证明如下:
.证明如下:
在直角三角形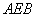 中,因为
中,因为 ,
, ,所以
,所以 .
.
在直角梯形 中,因为
中,因为 ,
, ,所以
,所以 ,
,
所以 .又因为
.又因为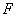 为
为 的中点,所以
的中点,所以 .
.
要使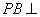 平面
平面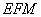 ,只需使
,只需使 .
.
因为 平面
平面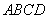 ,所以
,所以 ,又因为
,又因为 ,
, ,
,
所以 平面
平面 ,而
,而 平面
平面 ,所以
,所以 .
.
若 ,则
,则 ∽
∽ ,可得
,可得 .
.
由已知可求得 ,
, ,
, ,所以
,所以 .
.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
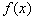 满足在集合
满足在集合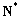 上的值域仍是集合
上的值域仍是集合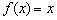 就是N函数.
就是N函数.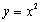 ,②
,②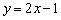 ,③
,③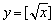 中,哪些是N函数?(只需写出判断结果);
中,哪些是N函数?(只需写出判断结果); 是否为N函数,并证明你的结论;
是否为N函数,并证明你的结论;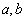 ,函数
,函数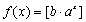 都不是N函数.
都不是N函数.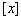 ”表示不超过
”表示不超过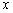 的最大整数)
的最大整数) R,
R, ”的否定是( )
”的否定是( ) B.不存在
B.不存在 R,
R,  R,
R, 的渐近线与抛物线
的渐近线与抛物线 相切,则此双曲线的离心率等于
相切,则此双曲线的离心率等于 B.
B.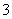 C.
C. D.
D.
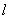 与圆
与圆 相交于
相交于 ,
, 两点,且线段
两点,且线段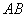 的中点坐标是
的中点坐标是 ,则直线
,则直线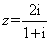 ,那么
,那么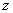 的虚部为( )
的虚部为( )
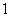
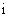
 中,点
中,点 ,
, ,若向量
,若向量 ,则实数
,则实数 _____.
_____. ,
, 和平面
和平面 ,
, ,使
,使 成立的一个充分条件是
成立的一个充分条件是 ,
,
 ,
, ,
,
 的图象
的图象