题目内容
6.四棱锥P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,AB=2,PA=$\frac{7}{2}$,若该四棱锥的所有项点都在同一球面上,则该球的表面积为( )| A. | $\frac{81π}{2}$ | B. | $\frac{81π}{4}$ | C. | 65π | D. | $\frac{65π}{2}$ |
分析 连结AC、BD,交于点E,则E是AC中点,取PC中点O,连结OE,推导出O是该四棱锥的外接的球心,球半径R=$\frac{1}{2}PC$,由此能求出该球的表面积.
解答  解:四棱锥P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,AB=2,PA=$\frac{7}{2}$,
解:四棱锥P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,AB=2,PA=$\frac{7}{2}$,
连结AC、BD,交于点E,则E是AC中点,取PC中点O,连结OE,
则OE∥PA,∴OE⊥平面ABCD,∴O到该四棱锥的所有顶点的距离相等,都为$\frac{1}{2}PC$,
∴O是该四棱锥的外接的球心,
该球半径R=$\frac{1}{2}PC$=$\frac{1}{2}\sqrt{P{A}^{2}+A{C}^{2}}$=$\frac{1}{2}\sqrt{\frac{49}{4}+8}$=$\frac{9}{4}$,
∴该球的表面积为S=4$π×(\frac{9}{4})^{2}$=$\frac{81π}{4}$.
故选:B.
点评 本题考查四面体的外接球的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
8.若$\frac{3π}{2}$≤α≤2π,则$\sqrt{1+sinα}$+$\sqrt{1-sinα}$等于( )
| A. | 2cos$\frac{α}{2}$ | B. | -2cos$\frac{α}{2}$ | C. | 2sin$\frac{α}{2}$ | D. | -2sin$\frac{α}{2}$ |
16.某中学进行了该学年度期末统一考试,该校为了了解高一年级1 000名学生的考试成绩,从中随机抽取了100名学生的成绩单,就这个问题来说,下面说法正确的是( )
| A. | 1 000名学生是总体 | B. | 每个学生是个体 | ||
| C. | 1 000名学生的成绩是一个个体 | D. | 样本的容量是100 |
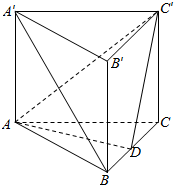 如图,三棱柱ABC-A′B′C′中,侧棱AA′⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点
如图,三棱柱ABC-A′B′C′中,侧棱AA′⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点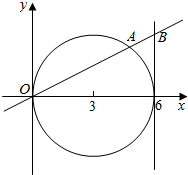 如图,已知动直线l交圆(x-3)2+y2=9于坐标原点O和点A,交直线x=6于点B;
如图,已知动直线l交圆(x-3)2+y2=9于坐标原点O和点A,交直线x=6于点B;