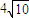题目内容
设2a是1+b和1-b的等比中项,则6a+4b的最大值为A.10 B.7 C.5 D.4
C 由2a是1+b和1-b的等比中项得4a2=1-b2,
∴4a2+b2=1.故可设(α∈R且α≠kπ(k∈Z)).
则6a+4b=3sinα+4cosα=5sin(α+φ),其中tanφ=
.
故6a+4b的最大值为5.
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
设2a是1+b和1-b的等比中项，则6a+4b的最大值为（ ）
| A、10 | ||
| B、7 | ||
| C、5 | ||
D、4
|
