Question

【题目】已知函数f (x)＝x2，g(x)＝x－1.

(1)若存在x∈R使f(x)<b·g(x)，求实数b的取值范围；

(2)设F(x)＝f(x)－mg(x)＋1－m－m2，且|F(x)|在上单调递增，求实数m的取值范围．

Answer 1

【答案】（1）b<0或b>4.（2）－1≤m≤0或m≥2.

【解析】试题分析:（1）化简不等式得x∈R，x2－bx＋b<0,由二次函数图像得,解得实数b的取值范围； （2）F(x)＝x2－mx＋1－m2，所以对称轴 ,再结合图像,得 ,解得实数m的取值范围．

试题解析：(1)x∈R，f(x)<bg(x)x∈R，x2－bx＋b<0

(－b)2－4b>0b<0或b>4.

(2)F(x)＝x2－mx＋1－m2，Δ＝m2－4(1－m2)＝5m2－4.

①当Δ≤0，即－≤m≤时，则必需

－≤m≤0.

②当Δ>0，即m<－或m>时，设方程F(x)＝0的根为x1，x2(x1<x2)．

若≥1，则x1≤0，即m≥2；

若≤0，则x2≤0，即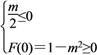

－1≤m<－；

综上所述：－1≤m≤0或m≥2.