题目内容
14.正方体ABCD-A1B1C1D1中,AD1与平面BDD1B1所成的角为30°.分析 设正方形ABCD的中心为O,连结OD1,则可证AC⊥平面BDD1B1,故而∠AD1O即为所求角.
解答  解:设正方形ABCD的中心为O,连结OD1,
解:设正方形ABCD的中心为O,连结OD1,
∵DD1⊥平面ABCD,AO?平面ABCD,
∴DD1⊥AO,又AO⊥BD,BD∩DD1=D,
∴AO⊥平面BB1D1D,
∴∠AD1O为AD1与平面BDD1B1所成的角,
∵AO=$\frac{1}{2}AC$,AC=AD1,
∴sin∠AD1O=$\frac{AO}{A{D}_{1}}=\frac{1}{2}$,
∴∠AD1O=30°.
故答案为:30°
点评 本题考查了棱柱的结构特征,线面角的计算,属于中档题.

练习册系列答案
相关题目
4.已知全集U={0,1,2,3,4,5,6,7},集合A={0,1,3,6},集合B={2,5,6,7},则(∁UB)∪A=( )
| A. | {0,1,2,3,4,5,6,7} | B. | {6} | C. | {2,4,5,6,7} | D. | {0,1,3,4,6} |
6.某地煤气公司规定,居民每个月使用的煤气费由基本月租费、保险费和超额费组成.每个月的保险费为3元,当每个月使用的煤气量不超过am3时,只缴纳基本月租费c元;如果超出这个使用量,超出的部分按b元/m3计费.
(1)请写出每个月的煤气费y(元)关于该月使用的煤气量x(m3)的函数解析式和该函数的定义域;
(2)如果某个居民7到9月份使用煤气与收费情况如表(其中,仅7月份煤气使用量未超过am3),请求出a,b,c的值.
(1)请写出每个月的煤气费y(元)关于该月使用的煤气量x(m3)的函数解析式和该函数的定义域;
(2)如果某个居民7到9月份使用煤气与收费情况如表(其中,仅7月份煤气使用量未超过am3),请求出a,b,c的值.
| 月 份 | 煤气使用量/m3 | 煤气费/元 |
| 7月 | 4 | 4 |
| 8月 | 25 | 14 |
| 9月 | 35 | 19 |
3.设A、B是非空数集,定义A*B={x|x∈A∪B且x∉A∩B},已知集合A={x|y=2x-x2},B={y|y=2x,x>0},则A*B=( )
| A. | [0,1]∪(2,+∞) | B. | [0,1)∪(2,+∞) | C. | (-∞,1] | D. | [0,2] |

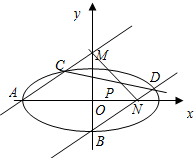 如图,分别过椭圆L的左顶点A(-3,0)和下顶点B且斜率为k(k>0)的两条直线l1和l2分别交椭圆L于点C,D,且l1交y轴于点M,l2交x轴于点N,且线段CD与线段MN相交于点P.当k=3时,△ABM是直角三角形.
如图,分别过椭圆L的左顶点A(-3,0)和下顶点B且斜率为k(k>0)的两条直线l1和l2分别交椭圆L于点C,D,且l1交y轴于点M,l2交x轴于点N,且线段CD与线段MN相交于点P.当k=3时,△ABM是直角三角形.