题目内容
 如图所示的正方体ABCD-A1B1C1D1中,过顶点B、D、C1作截面,则二面角B-DC1-C的平面角的余弦值是
如图所示的正方体ABCD-A1B1C1D1中,过顶点B、D、C1作截面,则二面角B-DC1-C的平面角的余弦值是
| ||
| 3 |
| ||
| 3 |
分析:以A为坐标原点,AB,AD,AA1分别为x,y,z轴正方向建立空间坐标系,根据正方体的几何特征,分别求出平面DC1C的一个法向量和平面BDC1的一个法向量,代入向量夹角公式,可得答案.
解答:解:以A为坐标原点,AB,AD,AA1分别为x,y,z轴正方向建立空间坐标系
设正方体ABCD-A1B1C1D1的棱长为a
则由正方体的几何特征可得
=(0,a,0)是平面DC1C的一个法向量;
设平面BDC1的法向量为
=(x,y,z)
由
=(-a,a,0),
=(0,a,a),
⊥
,
⊥
得
令x=1,则
=(1,1,-1)为平面BDC1的一个法向量
设二面角B-DC1-C的平面角为θ
则cosθ=
=
=
故答案为:
设正方体ABCD-A1B1C1D1的棱长为a
则由正方体的几何特征可得
| AD |
设平面BDC1的法向量为
| m |
由
| BD |
| BC1 |
| m |
| BD |
| m |
| BD |
|
令x=1,则
| m |
设二面角B-DC1-C的平面角为θ
则cosθ=
|
| ||||
|
|
| a | ||
a•
|
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查的知识点是二面角的平面角及求法,建立空间坐标系,将二面角问题转化为向量夹角问题是解答的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 如图所示,正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,G为DD1上一点,且D1G:GD=1:2,AC∩BD=O,求证:平面AGO∥平面D1EF.
如图所示,正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,G为DD1上一点,且D1G:GD=1:2,AC∩BD=O,求证:平面AGO∥平面D1EF. 如图所示,正方体ABCD-A1B1C1D1中,E、F分别是正方体ADD1A1和ABCD的中心,G是C1C的中点,设GF、C1F与AB所成的角分别为α、β,则α+β等于
如图所示,正方体ABCD-A1B1C1D1中,E、F分别是正方体ADD1A1和ABCD的中心,G是C1C的中点,设GF、C1F与AB所成的角分别为α、β,则α+β等于 在如图所示的坐标系中,已知P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体.其中AB=2,
在如图所示的坐标系中,已知P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体.其中AB=2,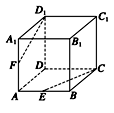
 如图所示,正方体ABCD-A1B1C1D1的棱长为1,点M在AB上,且AM=
如图所示,正方体ABCD-A1B1C1D1的棱长为1,点M在AB上,且AM=