题目内容
如图所示，正方体ABCD-A1B1C1D1中，E、F分别是AB、BC的中点，G为DD1上一点，且D1G：GD=1：2，AC∩BD=O，求证：平面AGO∥平面D1EF．
分析：证明两个平面平行，只需在一个平面内，找出两条相交直线与另一个平面平行即可．AO?平面D1EF，EH?平面D1EF，推出AO∥平面D1EF，
AO∩GO=O即可证明结论．
AO∩GO=O即可证明结论．
解答：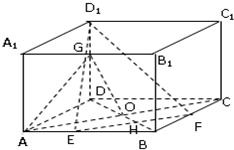
证明：如图所示，设EF∩BD=H，E、F分别是AB、BC的中点，G为DD1上一点，且D1G：GD=1：2，AC∩BD=O，在△DD1H中，
=
=
，
∴GO∥D1H，又GO?平面D1EF，D1H?平面D1EF，
∴GO∥平面D1EF，
在△BAO中，BE=EF，BH=HO，∴EH∥AO
AO?平面D1EF，EH?平面D1EF，∴AO∥平面D1EF，
AO∩GO=O，∴平面AGO∥平面D1EF．
证明：如图所示，设EF∩BD=H，E、F分别是AB、BC的中点，G为DD1上一点，且D1G：GD=1：2，AC∩BD=O，在△DD1H中，| DO |
| DH |
| 2 |
| 3 |
| DG |
| DD1 |
∴GO∥D1H，又GO?平面D1EF，D1H?平面D1EF，
∴GO∥平面D1EF，
在△BAO中，BE=EF，BH=HO，∴EH∥AO
AO?平面D1EF，EH?平面D1EF，∴AO∥平面D1EF，
AO∩GO=O，∴平面AGO∥平面D1EF．
点评：本题是中档题，考查平面与平面平行的判断，正确利用判断定理是证明立体几何题目的前提，考查逻辑推理能力．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
如图所示，正方体ABCD-A1B1C1D1中，E、F分别是正方体ADD1A1和ABCD的中心，G是C1C的中点，设GF、C1F与AB所成的角分别为α、β，则α+β等于
如图所示，正方体ABCD－A1B1C1D1的棱长为1，点M在AB上，且AM＝
AB，点P在平面ABCD上，且动点P到直线A1D1的距离的平方与P到点M的距离的平方差为1，在平面直角坐标系xAy中，动点P的轨迹方程是________．