题目内容
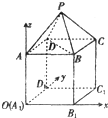在如图所示的坐标系中，已知P-ABCD是正四棱锥，ABCD-A1B1C1D1是正方体．其中AB=2，PA=| 6 |
（1，1，4）
（1，1，4）
．分析：如图所示．连接AC交BD于点Q，连接PQ，则PQ⊥底面ABCD．利用正四棱锥的性质即可得出|PQ|．
解答：解：如图所示．
连接AC交BD于点Q，连接PQ，则PQ⊥底面ABCD．
∴|PQ|=
=
=2．
∴P（1，1，4）．
故答案为（1，1，4）．
连接AC交BD于点Q，连接PQ，则PQ⊥底面ABCD．
∴|PQ|=
| |PA|2-|AQ|2 |
(
|
∴P（1，1，4）．
故答案为（1，1，4）．
点评：熟练掌握正四棱锥的性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
对于二次函数y=-2x2+5x
设变量x，y满足约束条件
对于二次函数y=-2x2+5x