题目内容
.如图,棱柱ABCD—A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°.(1)求异面直线BD和AA1所成的角;(2)求二面角D—A1A—C的平面角的余弦值;(3)在直线CC1上否存在点P,使BP∥平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.

[解析] 连接BD交AC于O,则BD⊥AC,连接A1O,在△AA1O中,AA1=2,AO=1,∠A1AO=60°,
∴A1O2=AA12+AO2-2AA1·AO·cos60°=3.∴AO2+A1O2=AA12.
∴A1O⊥AO,∵平面AA1C1C⊥平面ABCD,∴A1O⊥平面ABCD.
∴以OB、OC、OA1所在直线为x轴、y轴、z轴建立如图所示空间直角坐标系,则A(0,-1,0),B( ,0,0),C(0,1,0),D(-
,0,0),C(0,1,0),D(- ,0,0),A1(0,0,
,0,0),A1(0,0, ).
).
(1)∵ =(-2
=(-2 ,0,0),
,0,0), =(0,1,
=(0,1, ),
),
∴ ·
· =0×(-2
=0×(-2 )+1×0+
)+1×0+ ×0=0,
×0=0,
∴BD⊥AA1,即异面直线BD和AA1所成的角为90°.
(2)∵OB⊥平面AA1C1C,
∴平面AA1C1C的法向量n1=(1,0,0).
设n2=(x,y,z)是平面AA1D的一个法向量,则
 ∴
∴ 取n2=(1,
取n2=(1, ,-1).
,-1).
∴cos〈n1,n2〉= =
= .
.
∴二面角D—A1A—C的平面角的余弦值是 .
.
(3)假设在直线CC1上存在点P,使BP∥平面DA1C,
设 =λ
=λ ,P(x,y,z),
,P(x,y,z),
则(x,y-1,z)=λ(0,1, ).
).
∴P(0,1+λ, λ),
λ), =(-
=(- ,1+λ,
,1+λ, λ).
λ).
设n3=(x3,y3,z3)是平面DA1C1的一个法向量,则
∴ 不妨取n3=(1,0,-1).
不妨取n3=(1,0,-1).
又∵ ∥平面DA1C1,∴n3·
∥平面DA1C1,∴n3· =0,
=0,
∴- -
- λ=0,∴λ=-1,
λ=0,∴λ=-1,
即点P在C1C的延长线上,且使C1C=CP.


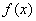 为定义域上的奇函数,
为定义域上的奇函数, 当
当 时,有
时,有 ,则
,则 的取值范围为 ( )
的取值范围为 ( ) B.
B.  C .
C .  D.
D. 
 的展开式中,
的展开式中, 的系数是 .
的系数是 .  和
和 ,且长为
,且长为 (B)
(B) (C)
(C) (D)
(D)
 ,则口袋中白球的个数为 …………………………………… …( )
,则口袋中白球的个数为 …………………………………… …( ) ,在第一次闭合出现红灯的条件下第二次闭合还出现红灯的概率是
,在第一次闭合出现红灯的条件下第二次闭合还出现红灯的概率是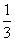 ,则两次闭合都出现红灯的概率为………………………………………( )
,则两次闭合都出现红灯的概率为………………………………………( )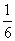 B.
B. C.
C. 
 ,
, ,如果
,如果 与
与 垂直,那么实数
垂直,那么实数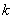 的值为 ___;
的值为 ___;