题目内容
a2,a5是方程x2-12x+27=0的两根,数列{an}是公差为正的等差数列,数列{bn}的前n项和为Tn,且Tn=1- bn(n∈N*).
bn(n∈N*).
(1)求数列{an},{bn}的通项公式;
(2)记cn=anbn,求数列{cn}的前n项和Sn.
解:(1)由a2+a5=12,a2•a5=27,且d>0,得a2=3,a5=9,∴d= =2,a1=1,∴an=2n-1,
=2,a1=1,∴an=2n-1,
在Tn=1- bn,令n=1,得b1=
bn,令n=1,得b1= ,当n≥2时,Tn=1-
,当n≥2时,Tn=1- bn 中,令 n=1得
bn 中,令 n=1得 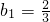 ,当n≥2时,
,当n≥2时,
Tn=1- bn,Tn-1=1-
bn,Tn-1=1-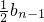 ,两式相减得
,两式相减得  ,
,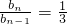 (n≥2),
(n≥2),
∴ =
=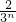 (n∈N+).
(n∈N+).
(2) =
= ,∴Sn=2(
,∴Sn=2( ),
),
∴ Sn=2(
Sn=2( ),
),
两式相减可解得 Sn=2- .
.
分析:(1)求出数列{an}的通项公式 an=2n-1,当n≥2时,求得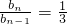 (n≥2),可得
(n≥2),可得  .
.
(2)由 =
= ,可得 Sn=2(
,可得 Sn=2( ),用错位相减法求数列的前n项和Sn.
),用错位相减法求数列的前n项和Sn.
点评:本题考查由递推关系求通项公式,用错位相减法求数列的前n项和.用错位相减法求数列的前n项和是解题的难点.
 =2,a1=1,∴an=2n-1,
=2,a1=1,∴an=2n-1,在Tn=1-
 bn,令n=1,得b1=
bn,令n=1,得b1= ,当n≥2时,Tn=1-
,当n≥2时,Tn=1- bn 中,令 n=1得
bn 中,令 n=1得 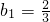 ,当n≥2时,
,当n≥2时,Tn=1-
 bn,Tn-1=1-
bn,Tn-1=1-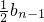 ,两式相减得
,两式相减得  ,
,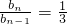 (n≥2),
(n≥2),∴
 =
=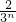 (n∈N+).
(n∈N+).(2)
 =
= ,∴Sn=2(
,∴Sn=2( ),
),∴
 Sn=2(
Sn=2( ),
),两式相减可解得 Sn=2-
 .
.分析:(1)求出数列{an}的通项公式 an=2n-1,当n≥2时,求得
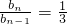 (n≥2),可得
(n≥2),可得  .
.(2)由
 =
= ,可得 Sn=2(
,可得 Sn=2( ),用错位相减法求数列的前n项和Sn.
),用错位相减法求数列的前n项和Sn.点评:本题考查由递推关系求通项公式,用错位相减法求数列的前n项和.用错位相减法求数列的前n项和是解题的难点.

练习册系列答案
相关题目