题目内容
5.已知函数f(x)=|x+1|(1)解不等式f(x)>4-|x-1|;
(2)已知a+b=1(a>0,b>0),若|x-m|-f(x)≤$\frac{4}{a}$+$\frac{1}{b}$(m>0)对任意的x∈R恒成立,求实数m的取值.
分析 (1)通过讨论x的范围,解各个区间上的不等式,求出不等式的解集即可;
(2)根据a+b=1,结合基本不等式的性质得到关于m的不等式,解出即可.
解答 解:(1)不等式f(x)>4-|x-1|,即|x+1|+|x-1|>4,
当x<-1时,不等式可化为-(x+1)-(x-1)>4,解得:x<-2,
当-1≤x≤1时,不等式可化为(x+1)-(x-1)>4不成立,
当x>1时,不等式可化为(x+1)+(x-1)>4,解得x>2,
∴原不等式的解集为{x|x<-2或x>2};
(2)$\frac{4}{a}$+$\frac{1}{b}$=($\frac{4}{a}$+$\frac{1}{b}$)(a+b)=5+$\frac{4b}{a}$+$\frac{a}{b}$≥9,
当且仅当a=$\frac{2}{3}$,b=$\frac{1}{3}$时等号成立,
由题意,则|x-m|-|x+1|≤9对任意x∈R恒成立,
又∵|x-m|-|x+1|≤|x-m-x-1|=|m+1|,
∴|m+1|≤9,
解之得:-10≤m≤8,
又m>0,∴0<m≤8,
∴m的取值范围为(0,8].
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,转化思想,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.执行如图所示的程序框图,输入θ=$\frac{π}{180}$,n=1,输出的结果是( )
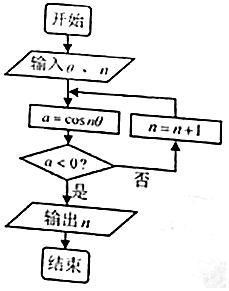

| A. | 90 | B. | 91 | C. | 180 | D. | 270 |
20.若数列{an}满足2an+an+1=0(n∈N*)且a3=-2,则a8的值为( )
| A. | -64 | B. | -32 | C. | $\frac{1}{64}$ | D. | 64 |
17.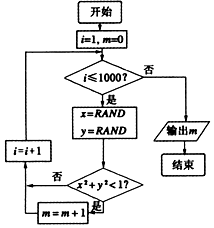 我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为781,则由此可估计π的近似值为( )
我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为781,则由此可估计π的近似值为( )
 我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为781,则由此可估计π的近似值为( )
我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为781,则由此可估计π的近似值为( )| A. | 3.119 | B. | 3.124 | C. | 3.132 | D. | 3.151 |
14.已知α为第四象限角,则$\frac{α}{2}$在第几象限( )
| A. | 二、四 | B. | 三、四 | C. | 二、三 | D. | 一、四 |
15.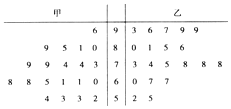 某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.
(1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个均“成绩优秀”的概率;
(2)由以上统计数据填写下面列联表,并判断是否有90%的把握认为“成绩优秀”与教学方式有关.
附:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
 某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.(1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个均“成绩优秀”的概率;
(2)由以上统计数据填写下面列联表,并判断是否有90%的把握认为“成绩优秀”与教学方式有关.
| 甲班(A方式) | 乙班(B方式) | 总 计 | |
| 成绩优秀 | 1 | 5 | 6 |
| 成绩不优秀 | 19 | 15 | 34 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
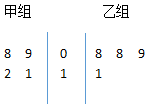 甲,乙两组各4名同学参加学校组织的“抗日战争历史知识知多少”抢答比赛,他们答对的题目个数用茎叶图表示,如图,中间一列的数字表示答对题目个数的十位数,两边的数字表示答对题目个数的个位数.
甲,乙两组各4名同学参加学校组织的“抗日战争历史知识知多少”抢答比赛,他们答对的题目个数用茎叶图表示,如图,中间一列的数字表示答对题目个数的十位数,两边的数字表示答对题目个数的个位数.