题目内容
已知向量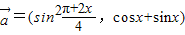 ,
,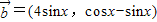 ,
,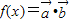
(1)求f(x)的解析式;
(2)求f(x)的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积.
【答案】分析:(1)利用三角函数的恒等变换以及两个向量数量积公式化简f(x)的解析式为2sinx+1.
(2)f(x)的图象与x轴的正半轴的第一个交点为 ,可得f(x)的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积
,可得f(x)的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积 ,运算求得结果.
,运算求得结果.
解答:解:(1) ----(2分)
----(2分)
=
∴f(x)=2sinx+1.------(7分)
(2)令f(x)=2sinx+1=0,可得sinx=- ,∴x=2kπ-
,∴x=2kπ- ,k∈z.
,k∈z.
f(x)的图象与x轴的正半轴的第一个交点为 ------(9分)
------(9分)
∴f(x)的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积
 =(-2cosx+x)
=(-2cosx+x) =(-2cos
=(-2cos +
+ )-(-2cos0+0)
)-(-2cos0+0)
= ------(13分)
------(13分)
点评:本题主要考查三角函数的恒等变换以及两个向量数量积公式的应用,利用定积分求图形的面积,化简f(x)的解析式为2sinx+1,是解题的关键,属于中档题.
(2)f(x)的图象与x轴的正半轴的第一个交点为
 ,可得f(x)的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积
,可得f(x)的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积 ,运算求得结果.
,运算求得结果.解答:解:(1)
 ----(2分)
----(2分)=

∴f(x)=2sinx+1.------(7分)
(2)令f(x)=2sinx+1=0,可得sinx=-
 ,∴x=2kπ-
,∴x=2kπ- ,k∈z.
,k∈z.f(x)的图象与x轴的正半轴的第一个交点为
 ------(9分)
------(9分)∴f(x)的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积
 =(-2cosx+x)
=(-2cosx+x) =(-2cos
=(-2cos +
+ )-(-2cos0+0)
)-(-2cos0+0)=
 ------(13分)
------(13分)点评:本题主要考查三角函数的恒等变换以及两个向量数量积公式的应用,利用定积分求图形的面积,化简f(x)的解析式为2sinx+1,是解题的关键,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目





 =
= ,
, ,
,
 ,若(∁RA)∪(∁RB)=∅,求实数a的取值范围.
,若(∁RA)∪(∁RB)=∅,求实数a的取值范围. 设函数
设函数
 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;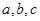 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若 △ABC的面积为
△ABC的面积为 ,求
,求 的值.
的值. 中,已知向量
中,已知向量 且
且 .
. 与
与 之间的关系式;
之间的关系式; ,求四边形
,求四边形 的面积.
的面积. ,且
,且
 的解析式和它的最小正周期;
的解析式和它的最小正周期; 的值域。
的值域。