题目内容
在R上定义运算?:x?y=x(1-y),若不等式(x-a)?(x+1)<1对任意实数x都成立,则实数a的取值范围______.
根据题中已知的新定义得:
(x-a)?(x+1)=(x-a)[1-(x+1)]=x(x-a),
代入不等式得:-x(x-a)<1,即x2-ax+1>0,
∵不等式对于任意实数x都成立,
∴△=(-a)2-4×1=a2-4<0,
解得:-2<a<2,
则实数a的取值范围是-2<a<2.
故答案为:-2<a<2
(x-a)?(x+1)=(x-a)[1-(x+1)]=x(x-a),
代入不等式得:-x(x-a)<1,即x2-ax+1>0,
∵不等式对于任意实数x都成立,
∴△=(-a)2-4×1=a2-4<0,
解得:-2<a<2,
则实数a的取值范围是-2<a<2.
故答案为:-2<a<2

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 :x
:x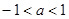 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.