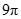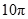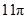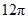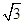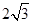题目内容
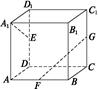
长方体ABCD—A1B1C1D1中,AA1=AB=2,AD=1, 点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角是( )
A.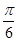 B.
B.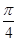 C.
C. 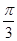 D.
D.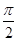

A.
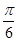 B.
B.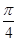 C.
C. 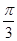 D.
D.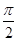
D
试题分析:连接B1G,则
 ,所以
,所以 就是异面直线A1E与GF所成的角,连接B1F,
就是异面直线A1E与GF所成的角,连接B1F,在
 中,
中, ,所以
,所以 ,
,所以
 .
.点评:找或做出异面直线所成的角,根据异面直线所成的角的定义要转化为求两条相交直线所成的角来解决.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
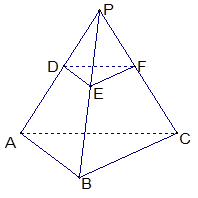
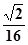 , 是否存在体积为V且各棱长均相等的平行六面体,使得它与棱台DEF-ABC有相同的棱长和,并且该平行六面体的一条侧棱与底面两条棱所成的角均为60°? 若存在,请具体构造出这样的一个平行六面体,并给出证明;若不存在,请说明理由.
, 是否存在体积为V且各棱长均相等的平行六面体,使得它与棱台DEF-ABC有相同的棱长和,并且该平行六面体的一条侧棱与底面两条棱所成的角均为60°? 若存在,请具体构造出这样的一个平行六面体,并给出证明;若不存在,请说明理由.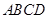 是矩形,
是矩形,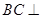 平面
平面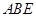 ,
,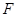 是
是 上一点,
上一点,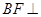 平面
平面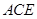 ,点
,点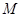 ,
,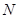 分别是
分别是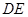 的中点.
的中点. 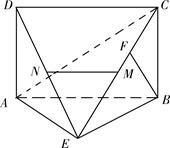
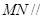 平面
平面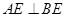 .
. 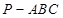 中,底面
中,底面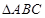 是边长为2的正三角形,
是边长为2的正三角形,  ⊥底面
⊥底面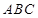 ,且
,且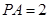 ,则此三棱锥外接球的半径为( )
,则此三棱锥外接球的半径为( )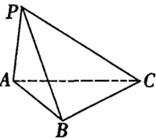
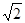

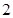
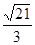
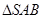 与直角梯形
与直角梯形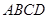 垂直,
垂直,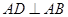 ,
,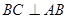 ,
,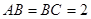 ,
,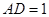 .若
.若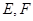 分别为
分别为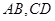 的中点.
的中点.
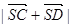 的值; (2)求面
的值; (2)求面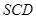 与面
与面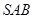 所成的二面角大小.
所成的二面角大小. 的各棱长都是2,E,F分别是
的各棱长都是2,E,F分别是 的中点,则EF的长是( )
的中点,则EF的长是( )