题目内容
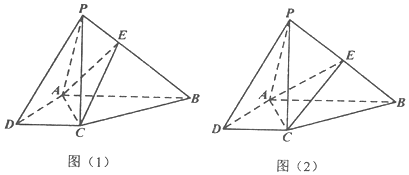
13.如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,AB⊥AD,AB=2AD=2CD=2,E是PB上的一点.(Ⅰ)求证:平面EAC⊥平面PBC;
(Ⅱ)如图(1),若$\overrightarrow{PE}$=$\frac{1}{3}$$\overrightarrow{PB}$,求证:PD∥平面EAC;
(Ⅲ)如图(2),若E是PB的中点,PC=2,求二面角P-AC-E的余弦值.
分析 (Ⅰ)取AB的中点M,连接CM,由已知可得:四边形CDAM是正方形,CM=MA=MB,可得AC⊥CB,PC⊥底面ABCD,于是PC⊥AC,即可证明AC⊥平面PBC;即得证
(Ⅱ)连接BD交AC于G,连接GE,可得$\frac{CD}{AB}=\frac{DG}{GB}=\frac{1}{2}$,PE:EB=1:2,即PD∥EG,PD∥平面EAC;
(Ⅲ)根据题意,由(Ⅰ)AC⊥平面PBC,可得∠PCE就是二面角P-AC-E的平面角.在△PCE中,由余弦定理得$cos∠PCE=\frac{P{C}^{2}+C{E}^{2}-P{E}^{2}}{2PC•CE}=\frac{\sqrt{6}}{3}$,即可
解答 解:(Ⅰ)证明:取AB的中点M,连接CM,
∵AM=$\frac{1}{2}$AB=1=CD=AD,AB⊥AD,AB∥CD,
∴四边形CDAM是正方形,CM=MA=MB,∴AC⊥CB,
∵PC⊥底面ABCD,∴PC⊥AC,又PC∩BC=C,
∴AC⊥平面PBC;又AC?∴面EAC⊥平面PBC.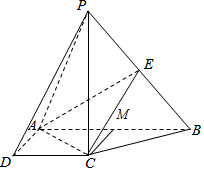
(Ⅱ)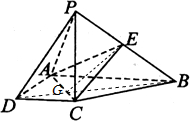 连接BD交AC于G,连接GE,
连接BD交AC于G,连接GE,
∵AB∥CD,AB=2CD,∴$\frac{CD}{AB}=\frac{DG}{GB}=\frac{1}{2}$,
∵$\overrightarrow{PE}$=$\frac{1}{3}$$\overrightarrow{PB}$,∴PE:EB=1:2,
∴PD∥EG,PD?平面EAC,EG?平面EAC;
∴PD∥平面EAC;
(Ⅲ) 由(Ⅰ)AC⊥平面PBC,∴∠PCE就是二面角P-AC-E的平面角.
∵PC=2,BC=$\sqrt{2}$,∴PB=$\sqrt{6}$.
∵E是PB的中点,∴$CE=PE=\frac{\sqrt{6}}{2}$.
在△PCE中,由余弦定理得$cos∠PCE=\frac{P{C}^{2}+C{E}^{2}-P{E}^{2}}{2PC•CE}=\frac{\sqrt{6}}{3}$,
∴二面角P-AC-E的余弦值为$\frac{\sqrt{6}}{3}$
点评 本题考查面面垂直、线面平行的判定,考查面面角,解题的关键是掌握面面垂直、线面平行的判定,属于中档题.

| A. | 64 | B. | 128 | C. | $\frac{64}{3}$ | D. | $\frac{128}{3}$ |
| A. | (-∞,lge-lg(lge)] | B. | (-∞,1] | C. | [1,lge-lg(lge)] | D. | [lge-lg(lge),+∞) |
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{7}$ | D. | $\frac{6}{7}$ |
| A. | [$\frac{1}{2}$,1) | B. | [$\frac{\sqrt{2}}{2},\frac{\sqrt{3}}{2}$] | C. | [$\frac{\sqrt{2}}{2}$,1] | D. | [$\frac{\sqrt{3}}{2}$,1) |

| A. | 24 | B. | 30 | C. | 48 | D. | 72 |