题目内容
△ABC中,sinA:sinB:sinC=3:5:7且△ABC的周长为30,则△ABC的面积为( )
A、
| ||||
B、
| ||||
C、13
| ||||
D、15
|
考点:正弦定理,余弦定理
专题:解三角形
分析:由条件利用正弦定理可得a:b:c=3:5:7,再根据△ABC的周长为30,求得三角形的三边长分别为a、b、c的值.由余弦定理求得cosC 的值,可得C=
,从而求得△ABC的面积为
ab•sinC 的值.
| 2π |
| 3 |
| 1 |
| 2 |
解答:
解:△ABC中,∵sinA:sinB:sinC=3:5:7,故由正弦定理可得a:b:c=3:5:7.
设a=3k,则b=5k,c=7k,再根据△ABC的周长为 3k+5k+7k=15k=30,可得k=2,
故三角形的三边长分别为:a=6,b=10,c=14.
由余弦定理可得cosC=
=-
,∴C=
,∴△ABC的面积为
ab•sinC=
×6×10×
=15
,
故选:D.
设a=3k,则b=5k,c=7k,再根据△ABC的周长为 3k+5k+7k=15k=30,可得k=2,
故三角形的三边长分别为:a=6,b=10,c=14.
由余弦定理可得cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
| 2π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
故选:D.
点评:本题主要考查正弦定理、余弦定理的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若如图所示的框图所给程序运行的结果S=
,那么判断框中可以填入的关于实数k的判断条件应是( )
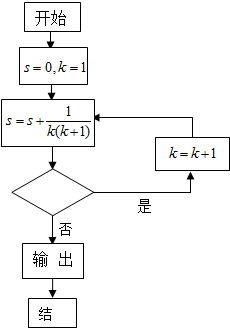
| 2010 |
| 2011 |

| A、k<2010 |
| B、k<2009 |
| C、k>2010 |
| D、k>2009 |
若抛物线y2=ax经过不等式组
表示的平面区域,则抛物线焦点的横坐标的取值范围是( )
|
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
函数y=3cos(2x+φ)的图象向右平移
后关于点(
,0)对称,那么|φ|的最小值为( )
| π |
| 3 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
、
满足|
|=1,|
+
|=3,则|
|的取值范围为( )
| a |
| b |
| a |
| a |
| b |
| b |
| A、[1,2] |
| B、[0,4] |
| C、[1,3] |
| D、[2,4] |
如图直角梯形ABCD中,AB∥DC,∠DAB=90°,DC=1,AB=3,AD=
,点E在边BC上且AC、AE、AB成等比数列,若
=λ
,则λ=( )
| 3 |
| CE |
| EB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
△ABC中B=
且sinA:sinC=3:1,则b:c的值为( )
| π |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、7 |
已知0<x<
,且t是大于O的常数,f(x)=
+
的最小值为9,则t的值为( )
| π |
| 2 |
| 1 |
| sinx |
| t |
| 1-sinx |
| A、4 | ||
| B、3 | ||
| C、2 | ||
D、
|