题目内容
18.已知sinθ=-$\frac{5}{13}$,且θ是第三象限角,则sin(θ+$\frac{π}{6}$)=$-\frac{{5\sqrt{3}+12}}{26}$.分析 由已知利用同角三角函数基本关系式可求cosθ,进而利用特殊角的三角函数值及两角和的正弦函数公式即可计算得解.
解答 解:∵sinθ=-$\frac{5}{13}$,且θ是第三象限角,
∴cosθ=-$\sqrt{1-si{n}^{2}θ}$=-$\frac{12}{13}$,
∴sin(θ+$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$sin$θ+\frac{1}{2}cosθ$=$\frac{\sqrt{3}}{2}×(-\frac{5}{13})$+$\frac{1}{2}×(-\frac{12}{13})$=$-\frac{{5\sqrt{3}+12}}{26}$.
故答案为:$-\frac{{5\sqrt{3}+12}}{26}$.
点评 本题主要考查了同角三角函数基本关系式,特殊角的三角函数值及两角和的正弦函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.在2L高产优质小麦种子中混入了一粒带白粉病的种子,从中随机取出10mL,则含有白粉病种子的概率是( )
| A. | $\frac{1}{20}$ | B. | $\frac{1}{50}$ | C. | $\frac{1}{100}$ | D. | $\frac{1}{200}$ |
8.已知直线l:x-$\sqrt{3}$y+6=0与圆x2+y2=12交于A,B两点,过A,B分别作l的垂线与x轴交于C,D两点,则|CD|=( )
| A. | $2\sqrt{3}$ | B. | 4 | C. | $4\sqrt{3}$ | D. | 6 |

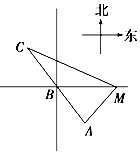 如图所示,已知A、B、C是一条直路上的三点,AB与BC各等于2km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看塔在正东方向,在点C处看见塔在南偏东60°方向,则塔M到直路ABC的最短距离为$\frac{14+10\sqrt{3}}{13}$.
如图所示,已知A、B、C是一条直路上的三点,AB与BC各等于2km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看塔在正东方向,在点C处看见塔在南偏东60°方向,则塔M到直路ABC的最短距离为$\frac{14+10\sqrt{3}}{13}$.