题目内容
10.若三角形ABC所在平面内一点M满足条件$\overrightarrow{CM}=\frac{1}{6}\overrightarrow{CB}+\frac{1}{3}\overrightarrow{CA}$,则S△MAC:S△MAB等于( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
分析 可作图,作向量$\overrightarrow{CD}=\frac{1}{6}\overrightarrow{CB},\overrightarrow{CE}=\frac{1}{3}\overrightarrow{CA}$,从而$\overrightarrow{CM}=\overrightarrow{CD}+\overrightarrow{CE}$,可设B到边AC的距离为d1,M到AC的距离为d2,d2也等于E到AC的距离,这样便可得出$\frac{{S}_{△MAC}}{{S}_{△ABC}}=\frac{1}{6}$,而同理可以得出$\frac{{S}_{△MBC}}{{S}_{△ABC}}=\frac{1}{3}$,从而便可得出S△MAC:S△MAB的值.
解答 解:如图,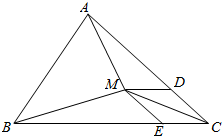
$\overrightarrow{CD}=\frac{1}{6}\overrightarrow{CB},\overrightarrow{CE}=\frac{1}{3}\overrightarrow{CA}$,则$\overrightarrow{CM}=\overrightarrow{CD}+\overrightarrow{CE}$;
令B到AC的距离为d1,M到AC的距离为d2,d2也是E到AC的距离,则$\frac{{{S_{△MAC}}}}{{{S_{△ABC}}}}=\frac{d_2}{d_1}=\frac{1}{6}$;
同理$\frac{{{S_{△MBC}}}}{{{S_{△ABC}}}}=\frac{1}{3}$;
∴$\frac{{S}_{△MAB}}{{S}_{△ABC}}=1-\frac{1}{6}-\frac{1}{3}=\frac{1}{2}$;
∴$\frac{{{S_{△MAC}}}}{{{S_{△MAB}}}}=\frac{1}{3}$.
故选A.
点评 考查向量数乘的几何意义,向量加法的平行四边形法则,相似三角形的比例关系,以及三角形的面积公式.

| A. | 3l-2m+$\frac{1}{3}n$ | B. | 3l-2m-$\frac{1}{3}n$ | C. | 3l-2m+3n | D. | 3l-2m-3n |
90 71 64 66 72 39 49 46 55 56 85 52 6l
80 66 67 78 70 51 65 42 73 77 58 67

(Ⅰ)请根据数据在答题卡的茎叶图中完成物理成绩统计;
(Ⅱ)请根据数据在答题卡上完成数学成绩的频数分布表及数学成绩的频率分布直方图;
| 数学成绩分组 | [50,60﹚ | [60,70﹚ | [70,80﹚ | [80,90﹚ | [90,100﹚ | [100,110﹚ | [110,120] |
| 频数 |

(Ⅲ)设上述样本中第i位考生的数学、物理成绩分别为xi,yi(i=1,2,3,…,25).通过对
样本数据进行初步处理发现:数学、物理成绩具有线性相关关系,得到:
$\overline{x}$=$\frac{1}{25}$$\sum_{i=1}^{25}$xi=86,$\overline{y}$=$\frac{1}{25}$$\sum_{i=1}^{25}$yi=64,$\sum_{i=1}^{25}$(xi-$\overline{x}$)(yi-$\overline{y}$)=4698,$\sum_{i=1}^{25}$(xi-$\overline{x}$)2=5524,$\frac{4698}{5524}$≈0.85.
求y关于x的线性回归方程,并据此预测当某考生的数学成绩为100分时,该考生的物理成绩(精确到1分).
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}\overline{x}$.
| A. | (-$\frac{1}{5}$,1) | B. | (-∞,-$\frac{1}{5}$)∪(1,+∞) | C. | [-$\frac{1}{5}$,1) | D. | (-∞,-$\frac{1}{5}$]∪[1,+∞) |
 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点P为体对角线的中点.若△PAC的正视图的最高点与侧视图的每一个顶点相连所得的几何体的体积为V1,正方体外接球的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为( )
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点P为体对角线的中点.若△PAC的正视图的最高点与侧视图的每一个顶点相连所得的几何体的体积为V1,正方体外接球的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为( )| A. | $\frac{1}{4π}$ | B. | $\frac{\sqrt{3}}{4π}$ | C. | $\frac{\sqrt{3}}{36π}$ | D. | $\frac{\sqrt{6}}{36π}$ |
| 不喜欢英语 | 喜欢英语 | 总计 | |
| 男生 | 40 | 18 | 58 |
| 女生 | 15 | 27 | 42 |
| 总计 | 55 | 45 | 100 |
(Ⅱ)用分层抽样方法在喜欢英语学科的学生中随机抽取5名,女学生应该抽取几名?
(Ⅲ)在上述抽取的5名学生中任取2名,求恰有1名学生为男性的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,
| p(K2≥k) | 0.100 | 0.050 | 0.025 | 0.01 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | $\frac{1}{10}$ | B. | $\frac{3}{25}$ | C. | $\frac{1}{15}$ | D. | $\frac{1}{30}$ |