题目内容
已知函数f(x)=
sin2x+sinxcosx-
(x∈R).
(1)求f(
)的值;
(2)求f(x)的单调增区间;
(3)若x∈(0,
),求f(x)的最大值.
| 3 |
| ||
| 2 |
(1)求f(
| π |
| 4 |
(2)求f(x)的单调增区间;
(3)若x∈(0,
| π |
| 2 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)根据三角函数的表达式,直接代入即可求f(
)的值;
(2)将三角函数进行化简,利用三角函数的单调性即可求f(x)的单调增区间;
(3)若x∈(0,
),求f(x)的最大值.
| π |
| 4 |
(2)将三角函数进行化简,利用三角函数的单调性即可求f(x)的单调增区间;
(3)若x∈(0,
| π |
| 2 |
解答:
解:(1)f(
)=
sin2
+sin
cos
-
=
.
(2)∵f(x)=
sin2x+sinxcosx-
=
×
+
sin2x-
=
sin2x-
cos2x,
∴f(x)=sin(2x-
),
∴令2kπ-
≤2x-
≤2kπ+
,k∈Z
则kπ-
≤x≤kπ+
,k∈Z,
∴[kπ-
,kπ+
](k∈Z)为f(x)的单调增区间;
(3)f(x)=
+
sin2x-
=
sin2x-
cos2x=sin(2x-
).
∵0<x<
,∴-
<2x-
<
.
∴当2x-
=
时,即x=
时,f(x)的最大值为1.
| π |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
(2)∵f(x)=
| 3 |
| ||
| 2 |
| 3 |
| 1-cos2x |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴f(x)=sin(2x-
| π |
| 3 |
∴令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
则kπ-
| π |
| 12 |
| 5π |
| 12 |
∴[kπ-
| π |
| 12 |
| 5π |
| 12 |
(3)f(x)=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
∵0<x<
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴当2x-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
点评:本题主要考查三角函数的图象和性质,利用辅助角公式将函数f(x)进行化简是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设a=0.20.3,b=0.30.3,c=log0.20.1,则a,b,c的大小关系为( )
| A、a>b>c |
| B、b>a>c |
| C、c>b>a |
| D、c>a>b |
 在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3600无后,逐步偿还转让费(不计息).在甲提供的资料中有:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需要各种开支2000元.
在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3600无后,逐步偿还转让费(不计息).在甲提供的资料中有:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需要各种开支2000元.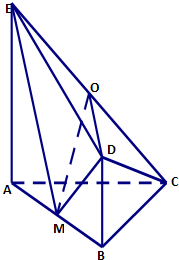 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AB=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AB=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD= 如图所示,正三棱柱ABC-A1B1C1中E,F,G,H分别是AB、AC、A1C1、A1B1的中点.
如图所示,正三棱柱ABC-A1B1C1中E,F,G,H分别是AB、AC、A1C1、A1B1的中点.