题目内容
4.已知f(x)=2|x+1|-|x-1|.(1)画出函数f(x)的图象;
(2)解不等式|f(x)|>1.
分析 (1)确定分段函数,即可画出函数f(x)的图象;
(2)根据图象可得|f(x)|=1时,x=-4或-1或$-\frac{2}{3}$或0,即可解不等式|f(x)|>1.
解答  解:(1)当x≥1时,f(x)=2(x+1)-(x-1)=x+3;
解:(1)当x≥1时,f(x)=2(x+1)-(x-1)=x+3;
当-1<x<1时,f(x)=2(x+1)-(1-x)=3x+1;
当x≤-1时,f(x)=-2(x+1)+(x-1)=-x-3,
所以$f(x)=\left\{\begin{array}{l}-x-3,x≤-1\\ 3x+1,-1<x<1\\ x+3,x≥1\end{array}\right.$;
(2)根据图象可得|f(x)|=1时,x=-4或-1或$-\frac{2}{3}$或0,
所以|f(x)|>1的解集为$({-∞,-4})∪({-1,-\frac{2}{3}})∪({0,+∞})$.
点评 本题考查绝对值不等式的解法,考查数形结合的数学思想,正确作出函数的图象是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
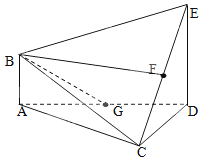 在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点,F是CE的中点.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点,F是CE的中点.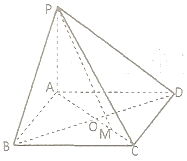 如图,已知四棱锥P-ABCD中,PA⊥BD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b,AC与BD交于点O,M为OC的中点.
如图,已知四棱锥P-ABCD中,PA⊥BD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b,AC与BD交于点O,M为OC的中点.