题目内容
4. 已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x2-2x,
已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x2-2x,(Ⅰ)求函数f(x)的解析式;
(Ⅱ)画出函数f(x)在R上的图象(不要求列表),并写出函数f(x)的单调区间(不用证明).
分析 (Ⅰ)根据函数奇偶性的对称性的性质即可求函数f(x)的解析式;
(Ⅱ)作出函数的图象,结合函数单调性的性质进行求解.
解答 解:(Ⅰ)设x<0,则-x>0…(1分)
∴f(-x)=x2+2x(2分)
∵函数f(x)是定义在R上的奇函数,
∴f(-x)=-f(x)(3分)
∴f(-x)=x2+2x=-f(x),
即f(x)=-x2-2x,x<0(4分)
又f(0)=0,
∴f(x)=$\left\{\begin{array}{l}{{x}^{2}-2x,}&{x≥0}\\{-{x}^{2}-2x,}&{x<0}\end{array}\right.$(6分)
(Ⅱ)作出对应的图象如图: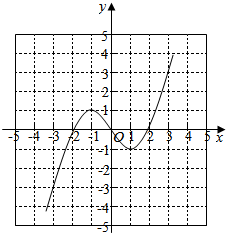 (9分)
(9分)
单调递增区间是:(-∞,-1]和[1,+∞); (11分)
单调递减区间是:(-1,1); (12分)
点评 本题主要考查函数解析式以及函数单调性的判断和求解,利用函数奇偶性的性质求出函数的解析式是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知集合U=R,P={x|x2-4x-5≤0},Q={x|x≥1},则P∩(∁UQ)( )
| A. | {x|-1≤x<5} | B. | {x|1<x<5} | C. | {x|1≤x<5} | D. | {x|-1≤x<1} |
12.在△ABC中,角A、B、C所对的边分别为a,b,c.若c=2,$C=\frac{π}{3}$,且a+b=3则△ABC的面积为( )
| A. | $\frac{{13\sqrt{3}}}{12}$ | B. | $\frac{{5\sqrt{3}}}{4}$ | C. | $\frac{5}{12}$ | D. | $\frac{{5\sqrt{3}}}{12}$ |
9.设全集U={1,a,5,7},集合M={1,a2-3a+3},∁UM={5,7},则实数a的值为( )
| A. | 1或3 | B. | 3 | C. | 1 | D. | -1或-3 |
16.等差数列{an}中,第1项为2,第2项为8,那么它的第3项为( )
| A. | -10 | B. | 10 | C. | 14 | D. | -12 |
14.直线l:y=kx+1与圆O:x2+y2=1相交于A,B两点,则“k=1”是“△OAB的面积为$\frac{1}{2}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
 若函数f(x)=ax(a>0,且a≠1)的图象如图,其中a为常数.则函数g(x)=xa(x≥0)的大致图象是( )
若函数f(x)=ax(a>0,且a≠1)的图象如图,其中a为常数.则函数g(x)=xa(x≥0)的大致图象是( )


