题目内容
根据下列条件,求圆的方程.
(1)经过坐标原点和点P(1,1),并且圆心在直线2x+3y+1=0上.
(2)过P(4,-2)、Q(-1,3)两点,且在y轴上截得的线段长为4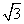 .
.
[解析] (1)显然,所求圆的圆心在OP的垂直平分线上,OP的垂直平分线方程为:
 又圆的半径r=|OC|=5,
又圆的半径r=|OC|=5,
∴所求圆的方程为(x-4)2+(y+3)2=25.
(2)设圆的方程为x2+y2+Dx+Ey+F=0.①
将P、Q点的坐标分别代入①得:
 令x=0,由①得y2+Ey+F=0.④
令x=0,由①得y2+Ey+F=0.④
由已知|y1-y2|=4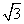 ,其中y1、y2是方程④的两根.
,其中y1、y2是方程④的两根.
∴(y1-y2)2=(y1+y2)2-4y1y2=E2-4F=48.⑤
解②、③、⑤组成的方程组,得
 故所求圆的方程为
故所求圆的方程为
x2+y2-2x-12=0,或x2+y2-10x-8y+4=0.

练习册系列答案
相关题目
 的图像不过第二象限时,
的图像不过第二象限时, 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
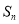 为等差数列
为等差数列 的前
的前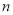 项和,已知
项和,已知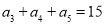 ,求
,求 ( )
( )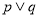 为真命题,则
为真命题,则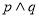 为真命题;②“
为真命题;②“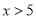 ”是“
”是“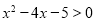 ”的充分不必要条件;③命题
”的充分不必要条件;③命题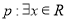 ,使得
,使得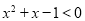 ,则
,则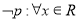 ,使得
,使得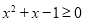 ;④命题“若
;④命题“若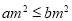 ,则
,则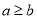 ”的否命题为真.其中错误的个数为( )
”的否命题为真.其中错误的个数为( ) ;
;  ;
;  ;
; ;
;  .
. ,M是CC1的中点,则异面直线AB1与A1M所成角为________.
,M是CC1的中点,则异面直线AB1与A1M所成角为________.