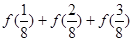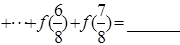题目内容
设数列 的前
的前 项和为
项和为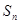 ,对任意的正整数
,对任意的正整数 ,都有
,都有 成立,记
成立,记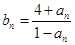 .(1)(1)求数列
.(1)(1)求数列 与数列
与数列 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为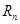 ,是否存在正整数
,是否存在正整数 ,使得
,使得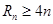 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数 ;若不存在,请说明理由.
;若不存在,请说明理由.
(3)记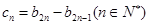 ,设数列
,设数列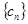 的前
的前 项和为
项和为 ,求证:对于
,求证:对于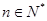 都有
都有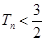
(1) ;(2)不存在,见解析;(3)见解析.
;(2)不存在,见解析;(3)见解析.
解析试题分析:(1)根据题中给的an=5Sn+1,继而可得an-1=5sn-1+1,两式子相减得,an-an-1=5an,因此 ,因而可得出an,bn的通项公式;(2)根据bn的通项公式,算出的前n项和为Rn,再计算出是否存在正整数k;(3)根据bn的通项公式,计算出cn的通项公式,再比较Tn与
,因而可得出an,bn的通项公式;(2)根据bn的通项公式,算出的前n项和为Rn,再计算出是否存在正整数k;(3)根据bn的通项公式,计算出cn的通项公式,再比较Tn与 的大小.
的大小.
(1)当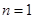 时,
时,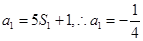 ,又
,又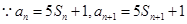 ,
,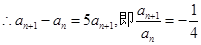 ,∴数列
,∴数列 是首项为
是首项为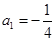 ,公比为
,公比为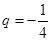 的等比数列,
的等比数列,
∴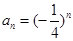 ,
, (2)不存在正整数
(2)不存在正整数 ,使得
,使得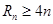 成立。证明:由(1)知
成立。证明:由(1)知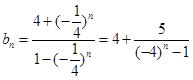

∴当n为偶数时,设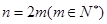 ,∴
,∴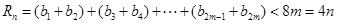
当n为奇数时,设
∴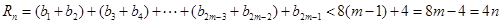
∴对于一切的正整数n,都有 ,∴不存在正整数
,∴不存在正整数 ,使得
,使得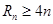 成立;(3)由
成立;(3)由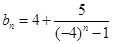 得
得
又 , 当
, 当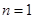 时,
时, ,当
,当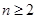 时,
时,
考点:数列递推式;数列的应用;数列的求和

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
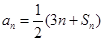 对一切正整数n成立
对一切正整数n成立 ,求数列
,求数列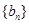 的前n项和
的前n项和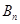 .
. 中,
中, ,
,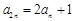 (
( ),
),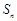 是数列
是数列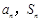 ;
;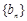 满足
满足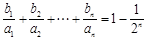 (
( 项和
项和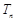 .
.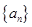 的前
的前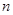 项和为
项和为 ,且
,且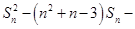
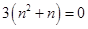 ,
, .
.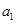 的值;
的值;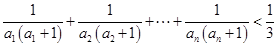 .
.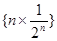 前
前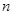 项和
项和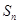 .
.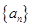 的前
的前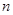 项和为
项和为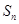 ,且
,且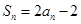 ,
,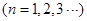 ;数列
;数列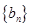 中,
中,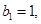 点
点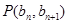 在直线
在直线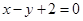 上.
上.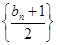 的前
的前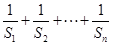 ;
;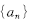 ,满足
,满足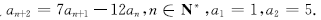
 均为等比数列;
均为等比数列;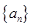 的通项公式
的通项公式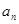 ;
;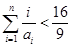 .
.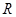 上的函数
上的函数 满足
满足 ,则
,则