题目内容
已知数列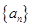 的前
的前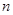 项和为
项和为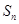 ,且
,且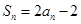 ,
,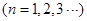 ;数列
;数列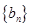 中,
中,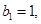 点
点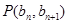 在直线
在直线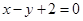 上.
上.
(1)求数列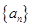 和
和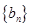 的通项公式;
的通项公式;
(2)设数列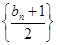 的前
的前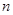 和为
和为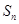 ,求
,求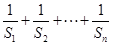 ;
;
(1) ,
, (2)
(2)
解析试题分析:(1)求数列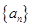 的通项公式用公式法即
的通项公式用公式法即 可推导数列
可推导数列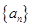 为等比数列,根据等比数列通项公式可求
为等比数列,根据等比数列通项公式可求 。求
。求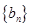 的通项公式也用公式法,根据已知条件可知数列
的通项公式也用公式法,根据已知条件可知数列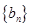 为等差数列,根据等差数列的通项公式可直接求得
为等差数列,根据等差数列的通项公式可直接求得 。(2)用列项相消法求和。
。(2)用列项相消法求和。
试题解析:解:(1)∵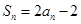 ,
,
∴当 时,
时, …2分
…2分
所以 ,即
,即
∴数列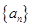 是等比数列.
是等比数列.
∵ ,∴
,∴
∴ . 5分
. 5分
∵点
 在直线
在直线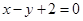 上,
上,
∴ ,
,
即数列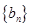 是等差数列,
是等差数列,
又 ,∴
,∴ .…7分
.…7分
(2)由题意可得 ,∴
,∴ , 9分
, 9分
∴ ,…10分
,…10分
∴ . 14分
. 14分
考点:1求数列的通向公式;2数列求和。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的前
的前 项和为
项和为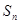 ,对任意的正整数
,对任意的正整数 成立,记
成立,记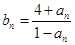 .(1)(1)求数列
.(1)(1)求数列 的通项公式;
的通项公式;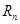 ,是否存在正整数
,是否存在正整数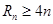 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数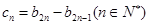 ,设数列
,设数列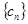 的前
的前 ,求证:对于
,求证:对于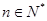 都有
都有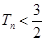
 的前
的前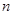 项和为
项和为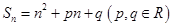 ,且
,且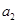 、
、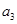
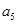 成等比数列.
成等比数列.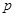 、
、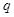 的值;
的值; 满足
满足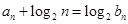 ,求数列
,求数列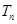 .
.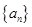 的前
的前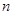 项和为
项和为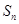 ,且
,且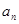 是
是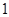 的等差中项,等差数列
的等差中项,等差数列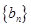 满足
满足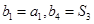
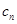 =
=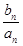 ,求数列
,求数列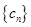 的前
的前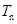 .
. 是函数
是函数 且
且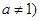 的图像上一点,等比数列
的图像上一点,等比数列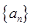 的前
的前 项的和为
项的和为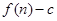 ;数列
;数列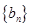
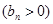 的首项为
的首项为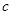 ,且前
,且前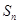 满足
满足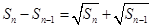
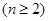 .
.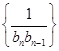 的前
的前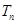 ,问
,问 的最小正整数
的最小正整数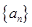 满足
满足 ,
, (
( ),则
),则 的值为 .
的值为 .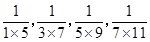 ,…
,… ,…
,…