题目内容
等差数列 中,
中, ,
,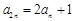 (
( ),
),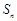 是数列
是数列 的前n项和.
的前n项和.
(1)求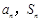 ;
;
(2)设数列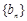 满足
满足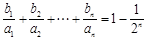 (
( ),求
),求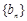 的前
的前 项和
项和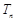 .
.
(1)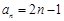 ,
,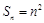 ;(2)
;(2)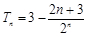 .
.
解析试题分析:(1)由等差数列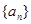 ,
, ,从而可将条件中的关系式
,从而可将条件中的关系式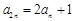 转化为关于公差
转化为关于公差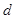 的方程:
的方程: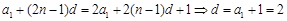 ,再由等差数列的通项公式及前
,再由等差数列的通项公式及前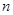 项和公式可知:
项和公式可知: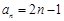 ,
,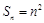 ;(2)根据关系式
;(2)根据关系式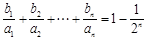 可知
可知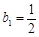 ,
,
当 时,
时, ,验证当
,验证当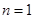 时,也有上述关系式,因此数列
时,也有上述关系式,因此数列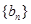 的通项公式为
的通项公式为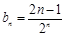 ,其通项公式为一个等差数列与一个等比数列的乘积,考虑采用错位相减法求其前
,其通项公式为一个等差数列与一个等比数列的乘积,考虑采用错位相减法求其前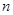 项和:
项和: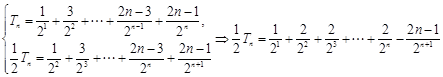 ,
,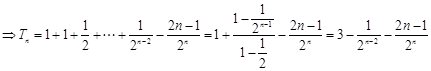
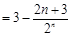 ,即
,即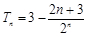 .
.
试题解析:(1)设 的公差为
的公差为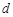 .由
.由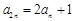 知,
知,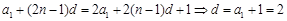 , 2分
, 2分
∴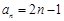 ,
,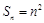 ; 4分
; 4分
(2)由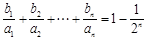 ,可知
,可知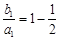 ,∴
,∴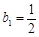 , 5分
, 5分
当 时,
时,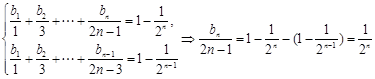 ,
,
当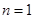 时,也符合
时,也符合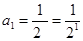 ,综上,
,综上,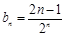 (
( ), 8分
), 8分
∴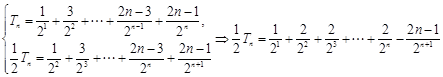 , 12分
, 12分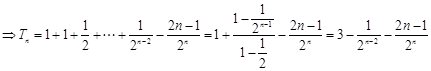
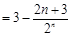 ,
,
即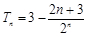 . 13分
. 13分
考点:1.等差数列的通项公式及其前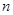 项和;2.数列的通项公式与错位相减法求数列的和.
项和;2.数列的通项公式与错位相减法求数列的和.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
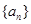 ,定义数列
,定义数列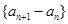 为数列
为数列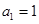 ,
,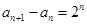 ,则
,则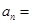 ______.
______. 的前n项和为
的前n项和为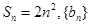 为等比数列,且
为等比数列,且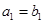 ,
,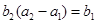 .
.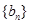 的通项公式;
的通项公式;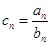 ,求数列
,求数列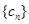 的前n项和
的前n项和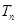 .
. 的前
的前 项和为
项和为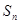 ,对任意的正整数
,对任意的正整数 成立,记
成立,记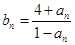 .(1)(1)求数列
.(1)(1)求数列 的通项公式;
的通项公式;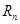 ,是否存在正整数
,是否存在正整数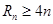 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数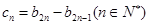 ,设数列
,设数列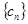 的前
的前 ,求证:对于
,求证:对于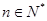 都有
都有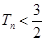
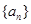 为正项递增数列,且
为正项递增数列,且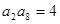 ,
,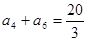 ,数列
,数列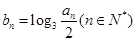 .
.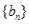 的通项公式;
的通项公式;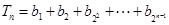 ,求
,求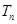 .
. 的前
的前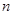 项和为
项和为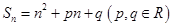 ,且
,且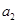 、
、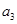
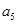 成等比数列.
成等比数列.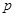 、
、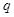 的值;
的值; 满足
满足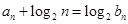 ,求数列
,求数列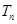 .
.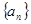 满足:
满足: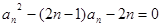 .
. ;
;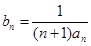 ,求数列
,求数列 项和
项和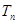 .
.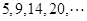 为“梯形数”.根据图形的构成,数列第
为“梯形数”.根据图形的构成,数列第 项
项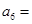 ; 第
; 第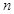 项
项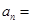 .
. 
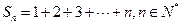 ,则
,则 的最大值为___★__.
的最大值为___★__.