题目内容
已知数列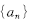 ,满足
,满足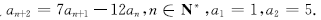
(I)求证:数列 均为等比数列;
均为等比数列;
(Ⅱ)求数列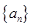 的通项公式
的通项公式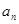 ;
;
(Ⅲ)求证: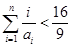 .
.
(I)详见试题解析;(Ⅱ) ;(Ⅲ)详见试题解析;.
;(Ⅲ)详见试题解析;.
解析试题分析:(I)将已知式变形成 从而得
从而得 都是等比数列;(Ⅱ)由(I)
都是等比数列;(Ⅱ)由(I) 都是等比数列,可得
都是等比数列,可得 消去
消去 即得数列
即得数列 的通项公式;(Ⅲ)
的通项公式;(Ⅲ) 故
故 因而只要证
因而只要证 利用错位相减法求和:
利用错位相减法求和: .最后利用放缩法证明不等式.
.最后利用放缩法证明不等式.
试题解析:(I)证明: 即
即 是首项为
是首项为 公比为
公比为 的等比数列. 2分
的等比数列. 2分
又 是首项为
是首项为 公比为
公比为 的等比数列. 4分
的等比数列. 4分
(Ⅱ)解:由(I)知 故
故 8分
8分
(Ⅲ)证明: 故
故 9分
9分
则
设 .
.
 12分
12分
故 . 13分
. 13分
考点:1.数列通项公式的求法;2.数列不等式的证明.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的前
的前 项和为
项和为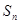 ,对任意的正整数
,对任意的正整数 成立,记
成立,记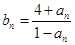 .(1)(1)求数列
.(1)(1)求数列 的通项公式;
的通项公式;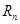 ,是否存在正整数
,是否存在正整数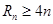 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数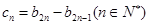 ,设数列
,设数列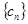 的前
的前 ,求证:对于
,求证:对于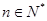 都有
都有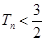
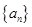 的前
的前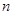 项和为
项和为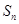 ,且
,且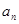 是
是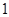 的等差中项,等差数列
的等差中项,等差数列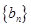 满足
满足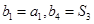
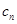 =
=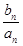 ,求数列
,求数列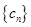 的前
的前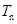 .
.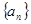 满足:
满足: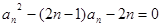 .
. ;
;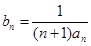 ,求数列
,求数列 项和
项和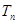 .
.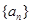 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列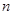 项和为
项和为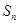 ,且满足
,且满足
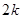 项和
项和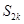 ;
;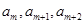 ,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数
,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数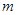 的值;若不存在,说明理由.
的值;若不存在,说明理由. 的前
的前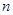 项和为
项和为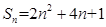 ,数列
,数列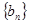 的首项
的首项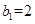 ,且点
,且点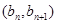 在直线
在直线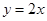 上.
上.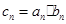 ,求数列
,求数列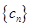 的前
的前 .
. 是函数
是函数 且
且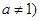 的图像上一点,等比数列
的图像上一点,等比数列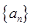 的前
的前 项的和为
项的和为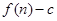 ;数列
;数列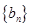
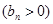 的首项为
的首项为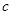 ,且前
,且前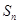 满足
满足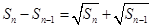
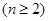 .
.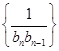 的前
的前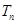 ,问
,问 的最小正整数
的最小正整数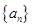 中,
中,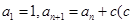 为常数,
为常数, ,且
,且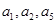 成公比不等于1的等比数列.
成公比不等于1的等比数列.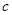 的值;
的值; ,求数列
,求数列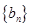 的前
的前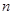 项和
项和 。
。