题目内容
用数学归纳法证明等式1+3+5+…+(2n﹣1)=n2(n∈N*)的过程中,第二步假设n=k时等式成立,则当n=k+1时应得到( )
A. 1+3+5+…+(2k+1)=k2 B. 1+3+5+…+(2k+1)=(k+1)2
C. 1+3+5+…+(2k+1)=(k+2)2 D. 1+3+5+…+(2k+1)=(k+3)2
B
考点: 数学归纳法.
专题: 阅读型.
分析: 首先由题目假设n=k时等式成立,代入得到等式1+3+5+…+(2k﹣1)=k2.当n=k+1时等式左边=1+3+5++(2k﹣1)+(2k+1)由已知化简即可得到结果.
解答: 解:因为假设n=k时等式成立,即1+3+5+…+(2k﹣1)=k2
当n=k+1时,等式左边=1+3+5+…+(2k﹣1)+(2k+1)=k2+(2k+1)=(k+1)2.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 x+θ)·cos(
x+θ)·cos( B.
B.
 :
: ,
, :
: ,若
,若 的取值范围
的取值范围 的反函数是( )
的反函数是( ) B.
B. 
 D.
D. 

 计算,每件2元,为使一年的运费和租金最省,每次进货量应为 ( )
计算,每件2元,为使一年的运费和租金最省,每次进货量应为 ( )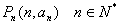 ,数列{an}的前n项和为Sn
,数列{an}的前n项和为Sn , 且Sn = 2n2 + 3n , 则直线
, 且Sn = 2n2 + 3n , 则直线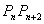 的一个方向向量的坐标可以是…………………………………………… ( )
的一个方向向量的坐标可以是…………………………………………… ( ) 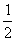 ) B.(-1, -1) C.(
) B.(-1, -1) C.( ) D. (
) D. ( , -1)
, -1)