题目内容
 设函数f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则
设函数f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则
- A.

- B.

- C.
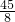
- D.-

B
分析:先根据函数f(x)是周期为2的奇函数得到 =-f(
=-f( )=-f(
)=-f( -2)=-f(
-2)=-f( );再结合0≤x≤1时对应的解析式即可求出结论.
);再结合0≤x≤1时对应的解析式即可求出结论.
解答:因为函数f(x)是周期为2的奇函数;
∴ =-f(
=-f( )=-f(
)=-f( -2)=-f(
-2)=-f( );
);
∵当0≤x≤1时,f(x)=2x(1-x),
∴ =-f(
=-f( )=-2×
)=-2× (1-
(1- )=-
)=- .
.
故选:B.
点评:本题主要考察函数的周期性以及奇偶性的综合应用.一般这种类型的题目常以选择或填空题的形式出现,比较基础.
分析:先根据函数f(x)是周期为2的奇函数得到
 =-f(
=-f( )=-f(
)=-f( -2)=-f(
-2)=-f( );再结合0≤x≤1时对应的解析式即可求出结论.
);再结合0≤x≤1时对应的解析式即可求出结论.解答:因为函数f(x)是周期为2的奇函数;
∴
 =-f(
=-f( )=-f(
)=-f( -2)=-f(
-2)=-f( );
);∵当0≤x≤1时,f(x)=2x(1-x),
∴
 =-f(
=-f( )=-2×
)=-2× (1-
(1- )=-
)=- .
.故选:B.
点评:本题主要考察函数的周期性以及奇偶性的综合应用.一般这种类型的题目常以选择或填空题的形式出现,比较基础.

练习册系列答案
相关题目
 设函数f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则
设函数f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则 ( )
( )




 的值为 .
的值为 .