题目内容
18.已知复数z1=1+$\sqrt{3}$i,|z2|=3,z1z2是正实数,则复数z2=z2=$\frac{3}{2}-\frac{3\sqrt{3}}{2}i$.分析 设复数z2=a+bi(a,b∈R),求出z1z2,再根据已知条件列出方程组,求解即可得答案.
解答 解:设复数z2=a+bi(a,b∈R),
z1z2=$(1+\sqrt{3}i)(a+bi)=(a-\sqrt{3}b)+(b+\sqrt{3}a)i$,
∵|z2|=3,z1z2是正实数,
∴$\left\{\begin{array}{l}{\sqrt{{a}^{2}+{b}^{2}}=3}\\{b+\sqrt{3}a=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=-\frac{3\sqrt{3}}{2}}\end{array}\right.$.
则复数z2=$\frac{3}{2}-\frac{3\sqrt{3}}{2}i$.
故答案为:z2=$\frac{3}{2}-\frac{3\sqrt{3}}{2}i$.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
10.已知函数f(x)=|x-1|,则与y=f(x)相等的函数是( )
| A. | g(x)=x-1 | B. | $h(x)=\left\{{\begin{array}{l}{x-1,}&{x>1}\\{1-x,}&{x<1}\end{array}}\right.$ | ||
| C. | $s(x)={(\sqrt{x-1})^2}$ | D. | $t(x)=\sqrt{{{(x-1)}^2}}$ |
7.函数f(x)=3x+2x-3的零点所在的区间是( )
| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |
 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则它的体积为16.
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则它的体积为16.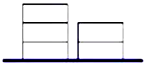 如图,在地上有同样大小的5块积木,一堆2个,一堆3个,要把积木一块一块的全部放到某个盒子里,每次只能取出其中一堆最上面的一块,则不同的取法有10种(用数字作答).
如图,在地上有同样大小的5块积木,一堆2个,一堆3个,要把积木一块一块的全部放到某个盒子里,每次只能取出其中一堆最上面的一块,则不同的取法有10种(用数字作答).