题目内容
13.(x2+1)(x+a)8的展开式中,x8的系数为113,则实数a的值为±2.分析 (x2+1)(x+a)8=(x2+1)$({x}^{8}+8{x}^{7}a+{∁}_{8}^{2}{x}^{6}{a}^{2}+…)$,可得x8的系数=1+${∁}_{8}^{2}{a}^{2}$,进而得出.
解答 解:(x2+1)(x+a)8=(x2+1)$({x}^{8}+8{x}^{7}a+{∁}_{8}^{2}{x}^{6}{a}^{2}+…)$,
∴x8的系数=1+${∁}_{8}^{2}{a}^{2}$=113,解得a=±2.
故答案为:±2.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.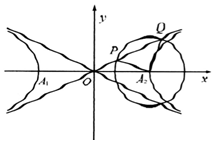 如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )
如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )
 如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )
如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
2.已知数列{an}满足an+1=$\frac{1}{{1-{a_n}}}$,若a1=$\frac{1}{2}$,则a2017=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -1 | D. | 1 |