题目内容
20.已知等比数列{an}的前n项和为Sn,则下列一定成立的是( )| A. | 若a3>0,则a2016>0 | B. | 若a4>0,则a2017>0 | ||
| C. | 若a3>0,则S2017>0 | D. | 若a4>0,则S2016>0 |
分析 设等比数列{an}的公比为q,利用通项公式与求和公式即可判断出结论.
解答 解:设等比数列{an}的公比为q,
若a3>0,则${a}_{1}{q}^{2}$>0,则a1>0.∴S2017=$\frac{{a}_{1}(1-{q}^{2017})}{1-q}$>0.a2016=${a}_{1}{q}^{2015}$与0的大小关系不确定.
若a4>0,则${a}_{1}{q}^{3}$>0,则a1与q同号,则a2017=${a}_{1}{q}^{2016}$,S2016=$\frac{{a}_{1}(1-{q}^{2016})}{1-q}$与0的大小关系不确定.
故选:C.
点评 本题考查了等比数列的通项公式与求和公式及其性质、不等式的性质与解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.将甲,乙等5位老师分别安排到高二的三个不同的班级任教,则每个班至少安排一人的不同方法数为( )
| A. | 150种 | B. | 180 种 | C. | 240 种 | D. | 540 种 |
7.数列0.9,0.99,0.999,…的一个通项公式是( )
| A. | 1+($\frac{1}{10}$)n | B. | -1+($\frac{1}{10}$)n | C. | 1-($\frac{1}{10}$)n | D. | 1-($\frac{1}{10}$)n+1 |
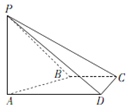 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,AD=2BC=2CD.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,AD=2BC=2CD. 心理健康教育老师对某班50个学生进行了心里健康测评,测评成绩满分为100分.成绩出来后,老师对每个成绩段的人数进行了统计,并得到如图4所示的频率分布直方图.
心理健康教育老师对某班50个学生进行了心里健康测评,测评成绩满分为100分.成绩出来后,老师对每个成绩段的人数进行了统计,并得到如图4所示的频率分布直方图. 如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC,设∠AOB=α(0<α<π).
如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC,设∠AOB=α(0<α<π). 在某校趣味运动会的颁奖仪式上,为了活跃气氛,大会组委会决定在颁奖过程中进行抽奖活动,用分层抽样的方法从参加颁奖仪式的高一、高二、高三代表队中抽取20人前排就座,其中高二代表队有5人.
在某校趣味运动会的颁奖仪式上,为了活跃气氛,大会组委会决定在颁奖过程中进行抽奖活动,用分层抽样的方法从参加颁奖仪式的高一、高二、高三代表队中抽取20人前排就座,其中高二代表队有5人. 满足
满足 ,则
,则 的最小值为_______.
的最小值为_______.