题目内容
若数列{an}的通项公式是 ,则
,则 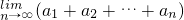 =________.
=________.

分析:先利用分组求和法求出a1+a2+…+an,然后求极限即可.
解答:a1+a2+…+an=(3-1+1)+[3-2+(-2)-1]+[3-3+(-2)-2]+…+[3-n+(-2)-n+1
=(3-1+3-2+…+3-n)+…+[1+(-2)-1+(-2)-2+…+(-2)-n+1]
=
 +
+ =
= +
+ ,
,所以
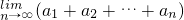 =
= =
= .
.故答案为:
 .
.点评:本题考查数列的极限奇数列的求和,熟练掌握数列求和的常用方法及有关结论是解决该类问题的基础.

练习册系列答案
相关题目