题目内容
14.已知两直线方程l1:mx+2y+8=0和l2:x+my+3=0,当m为何值时,(1)l1∥l2;
(2)l1⊥l2.
分析 (1)利用两直线平行时,一次项系数之比相等,但不等于常数项之比,求出m的值.
(2)当两条直线垂直时,斜率之积等于-1,解方程求出m的值.
解答 解:(1)两直线方程l1:mx+2y+8=0和l2:x+my+3=0,
∵m=0时,l1不平行l2,l1∥l2?$\frac{m}{1}=\frac{2}{m}≠\frac{8}{3}$,解得m=±$\sqrt{2}$.
(2)l1⊥l2 时,1×m+m×2=0,m=0,∴当m=0时,l1⊥l2.
点评 本题考查两直线垂直、平行的条件,体现了转化的数学思想.

练习册系列答案
相关题目
4.一个几何体的三视图如图所示,则该几何体的体积为( )
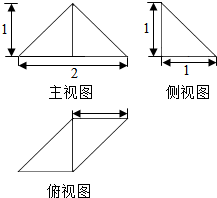

| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |