题目内容
【题目】(1)设![]() :实数x满足|x﹣m|<2,设
:实数x满足|x﹣m|<2,设![]() :实数x满足
:实数x满足![]() >1;若¬p是¬q的必要不充分条件,求实数m的取值范围
>1;若¬p是¬q的必要不充分条件,求实数m的取值范围
(2)已知p:函数f(x)=ln(x2﹣ax+3)的定义城为R,已知q:已知![]() 且
且![]() ,指数函数g(x)=(a﹣1)x在实数域内为减函数;若¬p∨q为假命题,求实数a的取值范围.
,指数函数g(x)=(a﹣1)x在实数域内为减函数;若¬p∨q为假命题,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)解绝对值不等式求得![]() 中
中![]() 的范围,解分式不等式求得
的范围,解分式不等式求得![]() 中
中![]() 的取值范围.由
的取值范围.由![]() 是
是![]() 的必要不充分条件知
的必要不充分条件知![]() 是
是![]() 的充分不必要条件,由此列不等式组,解不等式组求得
的充分不必要条件,由此列不等式组,解不等式组求得![]() 的取值范围.(2)根据
的取值范围.(2)根据![]() 的定义域为
的定义域为![]() 求得
求得![]() 为真时,
为真时,![]() 的取值范围.根据
的取值范围.根据![]() 的单调性求得
的单调性求得![]() 为假时
为假时![]() 的取值范围.
的取值范围.![]() 为假命题可知
为假命题可知![]() 真
真![]() 假,由此列不等式组,解不等式组求得
假,由此列不等式组,解不等式组求得![]() 的取值范围.
的取值范围.
(1)记![]() ,
,![]()
即![]()
由条件 ![]() 是
是![]() 的必要不充分条件知
的必要不充分条件知![]() 是
是![]() 的充分不必要条件,
的充分不必要条件,
从而有![]() 是
是![]() 的真子集,则
的真子集,则![]() ,
,
可得![]() ,故
,故![]()
(2)当![]() 为真命题时,函数
为真命题时,函数![]() 的定义域为
的定义域为![]() ,
,
则![]() 恒成立,即
恒成立,即![]() ,从而
,从而![]() ;
;
条件![]() 为假命题可知
为假命题可知![]() 真
真![]() 假,
假,
当![]() 为假命题时有
为假命题时有![]() 即
即![]()
从而当![]() 真
真![]() 假有
假有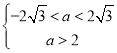
即![]() , 故
, 故![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


