题目内容
【题目】已知椭圆C:![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
,![]() ,过焦点
,过焦点![]() 的一条直线交椭圆于P,Q两点,若
的一条直线交椭圆于P,Q两点,若![]() 的周长为
的周长为![]() ,且长轴长与短轴长之比为
,且长轴长与短轴长之比为![]()
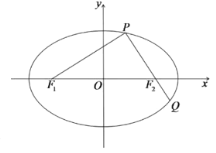
(1)求出椭圆的方程;
(2)若![]() ,求出弦长
,求出弦长![]() 的值;
的值;
(3)若![]() ,求出直线
,求出直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据焦点三角形周长、长短轴之比和![]() 可构造方程组求得
可构造方程组求得![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)设![]() ,由焦点三角形面积可构造方程求得
,由焦点三角形面积可构造方程求得![]() 点坐标,由此得到直线
点坐标,由此得到直线![]() 方程,与椭圆方程联立求得
方程,与椭圆方程联立求得![]() 点坐标,由两点间距离公式求得
点坐标,由两点间距离公式求得![]() ;
;
(3)设直线![]() 的方程为:
的方程为:![]() ,与椭圆方程联立得到韦达定理的形式;由平面向量线性运算可化简已知等式为
,与椭圆方程联立得到韦达定理的形式;由平面向量线性运算可化简已知等式为![]() ,由此得到
,由此得到![]() ,结合韦达定理构造方程求得
,结合韦达定理构造方程求得![]() ,进而得到直线方程.
,进而得到直线方程.
(1)由![]() 周长得:
周长得:![]() ,即
,即![]()
由长轴长与短轴长之比为![]() 得:
得:![]()
又![]() ,可解得:
,可解得:![]() ,
,![]() ,
,![]()
![]() 椭圆
椭圆![]() 的方程为
的方程为![]()
(2)设![]() ,则
,则![]()
![]()
![]() ,又
,又![]()
![]() ,即
,即![]()
![]()
![]() 或
或![]()
当![]() 时,直线
时,直线![]() 方程为
方程为![]() ,与椭圆方程联立得:
,与椭圆方程联立得:![]()
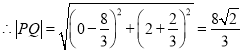
由椭圆对称性知,当![]() 时,
时,![]()
综上所述:![]()
(3)设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]()
![]()
![]()
![]() ,即
,即![]()
![]()
由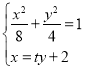 得:
得:![]()
则![]() ,
,![]()
![]()
即:![]() ,解得:
,解得:![]()
![]()
![]() 直线
直线![]() 的方程为:
的方程为:![]() 或
或![]()
即直线![]() 的方程为:
的方程为:![]() 或
或![]()

练习册系列答案
相关题目
【题目】已知函数f(x)=(x2﹣a)ex(a∈R).
(1)若函数f(x)有两个不同的极值点,求实数a的取值范围;
(2)当a=0时,若关于x的方程f(x)=m存在三个不同的实数根,求实数m的取值范围.
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
![]() 根据表中数据,问是否有
根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
![]() 已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|


