题目内容
【题目】已知一列非零向量![]() 满足:
满足:![]() ,
,![]() .
.
(1)写出数列![]() 的通项公式;
的通项公式;
(2)求出向量![]() 与
与![]() 的夹角
的夹角![]() ,并将
,并将![]() 中所有与
中所有与![]() 平行的向量取出来,按原来的顺序排成一列,组成新的数列
平行的向量取出来,按原来的顺序排成一列,组成新的数列![]() ,
,![]() ,
,![]() 为坐标原点,求点列
为坐标原点,求点列![]() 的坐标;
的坐标;
(3)令![]() (
(![]() ),求
),求![]() 的极限点位置.
的极限点位置.
【答案】(1)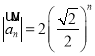 ;(2)
;(2)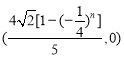 ;(3)
;(3)![]() .
.
【解析】
(1)得出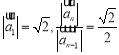 ,运用等比数列的定义判断,即可求出通项公式.
,运用等比数列的定义判断,即可求出通项公式.
(2)利用向量的数量积得出![]() 从而有:
从而有: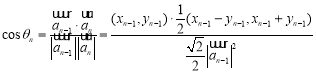 ,即可求得
,即可求得![]() 与
与![]() 的夹角;
的夹角;
先利用数学归纳法易证![]() 成立从而得出:
成立从而得出:![]() .结合等比数列的求得公式及数列的极限即可求得点列
.结合等比数列的求得公式及数列的极限即可求得点列![]() 的坐标;
的坐标;
(3)将![]() 分组,利用等比数列前
分组,利用等比数列前![]() 项和公式求出
项和公式求出![]() 的坐标,再求极限即可求出
的坐标,再求极限即可求出![]() 的极限点坐标.
的极限点坐标.
解:(1)![]()
![]()
![]()
![]() ,
,
![]()
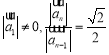
![]() 数列
数列![]() 是以
是以![]() ,
, 的等比数列,
的等比数列,
![]()
(2)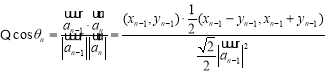
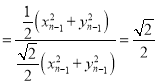 ,
,
![]() ,
,![]() ,
,
![]()
![]() 与
与![]() 的夹角为
的夹角为![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() 一般地,
一般地,![]() ,
,
用数学归纳法易证![]() 成立
成立![]()
![]() .
.
设![]()
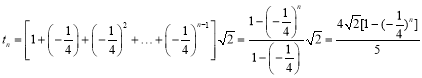 ;
;
![]() ,
,
所以点列![]() 的坐标为
的坐标为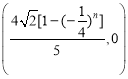
(3)由(2)知![]() 与
与![]() 的夹角为
的夹角为![]() ,
,
所以在![]() 中,与向量
中,与向量![]() 共线的向量为
共线的向量为![]() ,
,![]() ,
,![]() ,……
,……![]() 共
共![]() 个,
个,
与向量![]() 共线的向量为
共线的向量为![]() ,
,![]() ,
,![]() ,……
,……![]() 共
共![]() 个,
个,
与向量![]() 共线的向量为
共线的向量为![]() ,
,![]() ,
,![]() ,……
,……![]() 共
共![]() 个,
个,
与向量![]() 共线的向量为
共线的向量为![]() ,
,![]() ,
,![]() ,……
,……![]() 共
共![]() 个,
个,
![]()
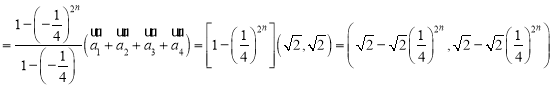

![]() 的极限点位置为
的极限点位置为![]() .
.

练习册系列答案
相关题目