题目内容
设a,b>0,且2a+b=1,则2
-4a2-b2的最大值是( )
| ab |
分析:先将2a+b=1两边平方,然后将2
-4a2-b2化简一下,然后利用二次函数求出ab的最值,从而可求出所求.
| ab |
解答:解:∵2a+b=1,
∴(2a+b)2=1,
∴S=2
-4a2-b2=4ab+2
-1,
∴ab有最大值时S有最大值.
∵2a+b=1,
∴2ab=b-b2=
-(b-
)2≤
,
∴当b=
时,2ab有最大值
∴当b=
时,a=
,S有最大值
+
-1=
故选C.
∴(2a+b)2=1,
∴S=2
| ab |
| ab |
∴ab有最大值时S有最大值.
∵2a+b=1,
∴2ab=b-b2=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴当b=
| 1 |
| 2 |
| 1 |
| 4 |
∴当b=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
故选C.
点评:本题主要考查了基本不等式,同时考查了运算求解的能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
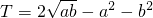 ,则当a=________且b=________时,Tmax=________.
,则当a=________且b=________时,Tmax=________.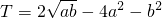 ,则当a=________且b=________时,Tmax=________.
,则当a=________且b=________时,Tmax=________. -4a2-b2的最大值是( )
-4a2-b2的最大值是( )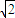 +1
+1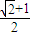
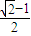
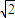 -1
-1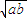 -4a2-b2的最大值是( )
-4a2-b2的最大值是( )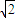 +1
+1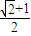
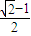
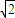 -1
-1