题目内容
(1)设a,b>0,且2a+b=1,设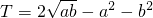 ,则当a=________且b=________时,Tmax=________.
,则当a=________且b=________时,Tmax=________.
(2)设a,b>0,且2a+b=1,设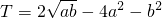 ,则当a=________且b=________时,Tmax=________.
,则当a=________且b=________时,Tmax=________.
解:(1)由题意a,b>0,且2a+b=1,
由于 ≤a+b,a2+b2≥2ab,当a=b时等号成立,
≤a+b,a2+b2≥2ab,当a=b时等号成立,
又2a+b=1,故有a=b= 时等号成立,
时等号成立,
所以Tmax=
故答案为 ,
, ,
,
(2)考察代数式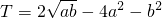 ,4a2+b2≥4ab,等号当且仅当2a=b时成立,
,4a2+b2≥4ab,等号当且仅当2a=b时成立,
此时有 =
= ≤
≤ ×
×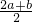 ,等号成立的条件是2a=b
,等号成立的条件是2a=b
又2a+b=1,故有2a=b= 时
时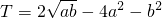 取到最大值
取到最大值
最大值为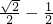 ,此时a=
,此时a= ,b=
,b=
故答案为 ,
, ,
,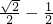
分析:(1)由题设中代数式的形式可以判断出,当 最大,而a2+b2取最小值时,T可取到最大值,由基本不等式即可求出最大值;
最大,而a2+b2取最小值时,T可取到最大值,由基本不等式即可求出最大值;
(2)由题设中代数式的形式可以判断出,当 最大,而4a2+b2取最小值时,T可取到最大值,由基本不等式即可求出最大值;
最大,而4a2+b2取最小值时,T可取到最大值,由基本不等式即可求出最大值;
点评:本题考查基本不等式在最值问题中的应用,解题的关键是熟练掌握基本不等式求最值的规则,一正,二定,三相等,解答本题的难点寻求等号成立的条件,本题易因为找不到等号成立的条件致使无法下手,注意总结基本不等式求最值时规律.
由于
 ≤a+b,a2+b2≥2ab,当a=b时等号成立,
≤a+b,a2+b2≥2ab,当a=b时等号成立,又2a+b=1,故有a=b=
 时等号成立,
时等号成立,所以Tmax=

故答案为
 ,
, ,
,
(2)考察代数式
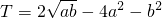 ,4a2+b2≥4ab,等号当且仅当2a=b时成立,
,4a2+b2≥4ab,等号当且仅当2a=b时成立,此时有
 =
= ≤
≤ ×
×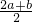 ,等号成立的条件是2a=b
,等号成立的条件是2a=b又2a+b=1,故有2a=b=
 时
时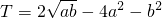 取到最大值
取到最大值最大值为
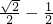 ,此时a=
,此时a= ,b=
,b=
故答案为
 ,
, ,
,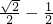
分析:(1)由题设中代数式的形式可以判断出,当
 最大,而a2+b2取最小值时,T可取到最大值,由基本不等式即可求出最大值;
最大,而a2+b2取最小值时,T可取到最大值,由基本不等式即可求出最大值;(2)由题设中代数式的形式可以判断出,当
 最大,而4a2+b2取最小值时,T可取到最大值,由基本不等式即可求出最大值;
最大,而4a2+b2取最小值时,T可取到最大值,由基本不等式即可求出最大值;点评:本题考查基本不等式在最值问题中的应用,解题的关键是熟练掌握基本不等式求最值的规则,一正,二定,三相等,解答本题的难点寻求等号成立的条件,本题易因为找不到等号成立的条件致使无法下手,注意总结基本不等式求最值时规律.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目