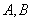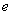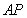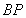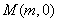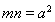题目内容
△AOB是边长为1的等边三角形,O是原点,AB⊥x轴,以O为顶点,且过A,B的抛物线的方程是( )
A、y2=
| ||||
B、y2=±
| ||||
C、y2=-
| ||||
D、y2=±
|
分析:设抛物线开口向右时方程为y2=2px,根据AB⊥x轴且等边△AOB的边长为1,算出点A的坐标并代入抛物线方程,算出2p=
,可得抛物线的方程为y2=
x.同理,当抛物线开口向左时方程为y2=-
x,从而得到答案.
| ||
| 6 |
| ||
| 6 |
| ||
| 6 |
解答:解:不妨设点A在x轴的上方,
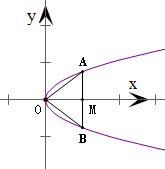 当抛物线开口向右时,设其方程为y2=2px,
当抛物线开口向右时,设其方程为y2=2px,
∵等边三角形△AOB是边长为1,AB⊥x轴,
∴设AB交x轴于点M,
则|OM|=
|AB|=
,|AM|=
|AB|=
,
由此可得点A的坐标为(
,
),
代入抛物线方程,得(
)2=2p×
,解得2p=
,
因此,抛物线的方程为y2=
x.
同理可得:抛物线开口向左时,其方程为y2=-
x.
综上所述,过A、B的抛物线的方程是y2=
x或y2=-
x.
故选:B
 当抛物线开口向右时,设其方程为y2=2px,
当抛物线开口向右时,设其方程为y2=2px,∵等边三角形△AOB是边长为1,AB⊥x轴,
∴设AB交x轴于点M,
则|OM|=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由此可得点A的坐标为(
| ||
| 2 |
| 1 |
| 2 |
代入抛物线方程,得(
| 1 |
| 2 |
| ||
| 2 |
| ||
| 6 |
因此,抛物线的方程为y2=
| ||
| 6 |
同理可得:抛物线开口向左时,其方程为y2=-
| ||
| 6 |
综上所述,过A、B的抛物线的方程是y2=
| ||
| 6 |
| ||
| 6 |
故选:B
点评:本题给出边长为1的正△AOB是抛物线的内接三角形,求抛物线的方程.着重考查了等边三角形的性质、抛物线的标准方程与简单几何性质等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
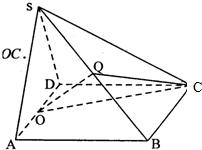 已知四棱锥S-ABCD中,△SAD是边长为2的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,O为AD的中点,Q为SB的中点,H为OQ的中点.
已知四棱锥S-ABCD中,△SAD是边长为2的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,O为AD的中点,Q为SB的中点,H为OQ的中点.