题目内容
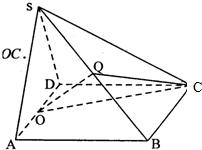 已知四棱锥S-ABCD中,△SAD是边长为2的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,O为AD的中点,Q为SB的中点,H为OQ的中点.
已知四棱锥S-ABCD中,△SAD是边长为2的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,O为AD的中点,Q为SB的中点,H为OQ的中点.(1)求证:OQ∥平面SCD;
(2)求二面角D-OC-Q的余弦值;
(3)证明:在△AOB内存在一点M,使HM⊥平面QOC.
分析:(1)做出辅助线,作辅助线的原则是有中点找中点,取SC中点R,连接QR,DR,根据线面平行的判定定理,在平面上找出一条直线与已知直线平行.
(2)连接SO,BO,在△OAB中,OB⊥OA,得到OA,OB,OS两两垂直,这样建立坐标系,写出要用的点的坐标,看出一个平面的法向量,再设出一个平面的法向量,根据两个向量的夹角得到二面角的余弦值.
(3)根据上一问设出的坐标系,写出要用到点的坐标,根据线与面垂直,得到关于x,y的值,经检验M坐标满足在△AOB内存在一点M,使HM⊥平面QOC.
(2)连接SO,BO,在△OAB中,OB⊥OA,得到OA,OB,OS两两垂直,这样建立坐标系,写出要用的点的坐标,看出一个平面的法向量,再设出一个平面的法向量,根据两个向量的夹角得到二面角的余弦值.
(3)根据上一问设出的坐标系,写出要用到点的坐标,根据线与面垂直,得到关于x,y的值,经检验M坐标满足在△AOB内存在一点M,使HM⊥平面QOC.
解答:解:(1)取SC中点R,连接QR,DR,
由题意知OD∥BC,OD=
BC,QR∥BC,QR=
BC,QR∥OD,QR=OD
所以OQ∥DR,又OQ?平面SCD,DR?平面SCD
所以OQ∥平面SCD
(2)连接SO,BO,在△OAB中,OB⊥OA
又因为平面SAD⊥平面ABCD,
所以OS⊥AD,
所以OS⊥平面ABCD
所以OA,OB,OS两两垂直
如图,建系O(0,0,0),S(0,0,
),B(0,
,0),C(-2,
,0)Q(0,
,
)
平面OCD的法向量为
=(0,0,
)
设
=(x,y,z)为平面OQC的一个法向量
由
得
取z=1得cos<
,
>=
=
二面角D-OC-Q的余弦值为-
(3)设点M(x,y,0),H(0,
,
),
=(x,y-
,-
),HM⊥平面QOC,
∴
在△AOB内部区域满足不等式组
经检验M坐标满足
在△AOB内存在一点M,使HM⊥平面QOC
由题意知OD∥BC,OD=
| 1 |
| 2 |
| 1 |
| 2 |
所以OQ∥DR,又OQ?平面SCD,DR?平面SCD
所以OQ∥平面SCD
(2)连接SO,BO,在△OAB中,OB⊥OA
又因为平面SAD⊥平面ABCD,
所以OS⊥AD,
所以OS⊥平面ABCD
所以OA,OB,OS两两垂直
如图,建系O(0,0,0),S(0,0,
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| ||
| 2 |

平面OCD的法向量为
| OS |
| 3 |
设
| n |
由
|
|
取z=1得cos<
| n |
| OS |
| ||||
|
|
2
| ||
| 11 |
二面角D-OC-Q的余弦值为-
2
| ||
| 11 |
(3)设点M(x,y,0),H(0,
| ||
| 4 |
| ||
| 4 |
| HM |
| ||
| 4 |
| ||
| 4 |
∴
|
在△AOB内部区域满足不等式组
|
经检验M坐标满足
在△AOB内存在一点M,使HM⊥平面QOC
点评:本题考查利用空间向量解决几何体中的夹角和距离的问题,本题解题的关键是建立合适的坐标系,把逻辑性很强的理论推导转化成数字的运算,降低了题目的难度.

练习册系列答案
相关题目
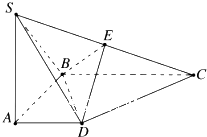 已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=