题目内容
.



解:⑴ 令
令 ,得
,得 ,
,
 区间
区间 分别单调增,单调减,单调增,…………2分
分别单调增,单调减,单调增,…………2分
于是当 时,有极大值
时,有极大值
 极小值
极小值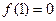 ,…………4分
,…………4分
⑵由(1)知 区间
区间 分别单调增,单调减,单调增,
分别单调增,单调减,单调增,
所以当 时
时 ,特别当
,特别当 时,有
时,有 ;6分
;6分
当 时,
时, ,则
,则 ,………8分
,………8分
所以对任意的 ,
, ……9分
……9分
⑶由已知得
 在
在 上恒成立,
上恒成立,
 得
得 时,
时, ,
, 单调减;
单调减;
 时,
时, ,
, 单调增;故
单调增;故 时,函数
时,函数 取到最小值,从而
取到最小值,从而 ;…11分
;…11分
同样的, 在
在 上恒成立,由
上恒成立,由
得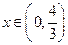 时,
时, ,
, 时,
时, ,故
,故 时,函数
时,函数 取到最小值.
取到最小值.
从而 ,………13分
,………13分
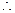
 由
由 的唯一性知
的唯一性知 ,
, .……14分
.……14分
 令
令 ,得
,得 ,
, 区间
区间 分别单调增,单调减,单调增,…………2分
分别单调增,单调减,单调增,…………2分于是当
 时,有极大值
时,有极大值
 极小值
极小值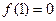 ,…………4分
,…………4分⑵由(1)知
 区间
区间 分别单调增,单调减,单调增,
分别单调增,单调减,单调增,所以当
 时
时 ,特别当
,特别当 时,有
时,有 ;6分
;6分当
 时,
时, ,则
,则 ,………8分
,………8分所以对任意的
 ,
, ……9分
……9分⑶由已知得

 在
在 上恒成立,
上恒成立, 得
得 时,
时, ,
, 单调减;
单调减; 时,
时, ,
, 单调增;故
单调增;故 时,函数
时,函数 取到最小值,从而
取到最小值,从而 ;…11分
;…11分同样的,
 在
在 上恒成立,由
上恒成立,由
得
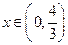 时,
时, ,
, 时,
时, ,故
,故 时,函数
时,函数 取到最小值.
取到最小值.从而
 ,………13分
,………13分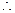
 由
由 的唯一性知
的唯一性知 ,
, .……14分
.……14分略

练习册系列答案
相关题目
 (b、c、d为常数),当
(b、c、d为常数),当 时,
时, 只有一个实根,当
只有一个实根,当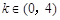 时,
时, 有2个极值点;②函数
有2个极值点;②函数 有一个相同的实根;④
有一个相同的实根;④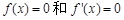 有一个相同的实根。
有一个相同的实根。 ,其图象在
,其图象在 处的切线方程为
处的切线方程为 .
. 的解析式;
的解析式; 的图象与
的图象与 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数 的取值范围;
的取值范围;
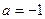 时,求函数的单调区间。
时,求函数的单调区间。 时,讨论函数的单调增区间。
时,讨论函数的单调增区间。 ,使
,使 ,函数有最小值-3?
,函数有最小值-3?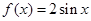 ,则
,则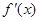 等于( ).
等于( ). 



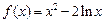 .
.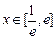 时,不等式
时,不等式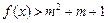 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;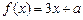 在区间[
在区间[ 1,3]上恰好有两个相异的实根,求实数
1,3]上恰好有两个相异的实根,求实数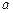 的取值范围.
的取值范围. 作曲线
作曲线 的切线,则切线斜率为 .
的切线,则切线斜率为 .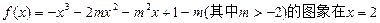 处的切线与直线
处的切线与直线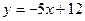 平行.
平行. 的值;
的值; 在区间[0,1]的最小值;
在区间[0,1]的最小值; ,根据上述(I)
,根据上述(I) 、(II)的结论,证明:
、(II)的结论,证明:
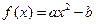 在区间
在区间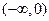 内是减函数,则
内是减函数,则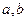 应满足( )
应满足( ) 且
且
 且
且
