题目内容
6.“x<1”是“log${\;}_{\frac{1}{2}}}$x>0”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 根据对数函数的性质和充要条件的定义,分析判断“x<1”⇒“${log_{\frac{1}{2}}}x>0$”和“${log_{\frac{1}{2}}}x>0$”⇒“x<1”的真假,可得答案.
解答 解:当“x<1”时,x可能小于等于0,此时“${log_{\frac{1}{2}}}x>0$”无意义,
当“${log_{\frac{1}{2}}}x>0$”时,0<x<1,此时“x<1”成立,
故“x<1”是“${log_{\frac{1}{2}}}x>0$”的必要而不充分条件,
故选:B.
点评 本题考查的知识点是充要条件,熟练掌握充要条件的定义是解答的关键.

练习册系列答案
相关题目
16.若存在实数x=x0,使得不等式ax>a-1不成立,则实数a的取值范围是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-∞,+∞) |
11.记函数f(x)的导函数为f′(x),若f(x)对应的曲线在点(x0,f(x0))处的切线方程为y=-x+1,则( )
| A. | f′(x0)=2 | B. | f′(x0)=1 | C. | f′(x0)=0 | D. | f′(x0)=-1 |
18.已知集合A={x|-2<x<1},B={x|x2-2x≤0},则A∩B=( )
| A. | {x|0<x<1} | B. | {x|0≤x<1} | C. | {x|-1<x≤1} | D. | {x|-2<x≤1} |
 如图⊙O1与⊙O2相交于A、B两点,过A点的直线分别与⊙O1、⊙O2相文于C、D两点,以C、D为切点分别作两圆的切线相交于点E.
如图⊙O1与⊙O2相交于A、B两点,过A点的直线分别与⊙O1、⊙O2相文于C、D两点,以C、D为切点分别作两圆的切线相交于点E. 和点
和点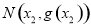 分别是函数
分别是函数 和
和 图象上的点,且
图象上的点,且 ,若直线
,若直线 轴,则
轴,则 两点间的距离的最小值为( )
两点间的距离的最小值为( ) 在
在 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.