题目内容
8.已知(1-2x)2016=a0+a1x+a2x2+…+a2016x2016.求:(1)a0+a1+a2+…+a2016的值;
(2)a0+a2+a4+…++a2014+a2016的值.
分析 (1)利用x=1代入求解即可.
(2)利用x=1与x=-1,然后求解即可.
解答 解:(1-2x)2016=a0+a1x+a2x2+…+a2016x2016.
(1)令x=1,(1-2)2016=a0+a1+a2+…+a2016=1;
(2)当x=-1时,32016=a0-a1+a2+…+a2016…①,
由(1)a0+a1+a2+…+a2016=1…②,①+②可得:a0+a2+a4+…++a2014+a2016=$\frac{1}{2}$×32016+$\frac{1}{2}$.
点评 本题考查二项式定理的应用,赋值法的应用,考查计算能力.

练习册系列答案
相关题目
18.已知线性回归直线方程是$\stackrel{∧}{y}$=1.23x+0.08,求m的值.
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | m | 6.5 | 7.0 |
16.若实数x、y满足不等式组$\left\{\begin{array}{l}{x-y+5≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$,且z=ax+y仅在点P(-$\frac{5}{2}$,$\frac{5}{2}$)处取得最小值,则a的取值范围为( )
| A. | 0<a<1 | B. | a>1 | C. | a≥1 | D. | a≤0 |
17.若13sinα+5cosβ=9,13cosα+5sinβ=15,则sin(α+β)的值为( )
| A. | $\frac{56}{65}$ | B. | $\frac{33}{65}$ | C. | $\frac{5}{6}$ | D. | $\frac{16}{65}$ |
8.已知函数f(x)=(a2-1)x是其定义域上的单调减函数,则实数a的取值集合为( )
| A. | {a|0<a<1} | B. | $\left\{{\left.a\right|1<a<\sqrt{2}}\right\}$ | ||
| C. | $\left\{{\left.a\right|-\sqrt{2}<a<-1}\right.$或$\left.{1<a<\sqrt{2}}\right\}$ | D. | $\left\{{\left.a\right|-\sqrt{2}<a<\sqrt{2}}\right\}$ |
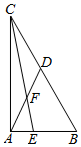 已知$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,|$\overrightarrow{AB}-\overrightarrow{AC}$|=2,D是边BC的中点,$\overrightarrow{AE}$=$\frac{1}{3}\overrightarrow{AB}$
已知$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,|$\overrightarrow{AB}-\overrightarrow{AC}$|=2,D是边BC的中点,$\overrightarrow{AE}$=$\frac{1}{3}\overrightarrow{AB}$