题目内容
10.已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,则y12+y22的最小值是( )| A. | 8 | B. | 32 | C. | 16 | D. | 4 |
分析 先根据点P设直线方程与抛物线方程联立消去y,根据韦达定理求得x1x2=16,进而根据均值不等式y12+y22=4(x1+x2)≥8$\sqrt{{x}_{1}{x}_{2}}$,求得答案.
解答 解:设直线方程为y=k(x-4),与抛物线方程联立消去y得k2x2-(8k2+4)x+16k2=0
∴x1x2=16
显然x1,x2>0,又y12+y22=4(x1+x2)≥8$\sqrt{{x}_{1}{x}_{2}}$=32,
当且仅当x1=x2=4时取等号,此时k不存在.
故选B.
点评 本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
相关题目
20.若集合P={-2,0,2},i是虚数单位,则( )
| A. | 2i∈P | B. | $\frac{2}{i}$∈P | C. | ($\sqrt{2}$i)2∈P | D. | $\frac{2}{{i}^{3}}$∈P |
5.从2 012名学生中选取50名学生参加数学竞赛,若采用下面的方法选取:先用简单随机抽样从2 012人中剔除12人,剩下的2 000人再按系统抽样的方法抽取50人,则在2 012人中,每人入选的概率( )
| A. | 不全相等 | B. | 均不相等 | ||
| C. | 都相等,且为$\frac{1}{40}$ | D. | 都相等,且为$\frac{25}{1006}$ |
12.函数f(x)=$\left\{\begin{array}{l}{x+1(x≥0)}\\{{x}^{2}+2x+1(x<0)}\end{array}\right.$,若矩形ABCD的顶点A、D在x轴上,B、C在函数y=f(x)的图象上,且A(1,0),则点D的坐标为( )
| A. | (-2,0) | B. | (-1-$\sqrt{2}$,0) | C. | (-1,0) | D. | (-$\frac{1}{2}$,0) |
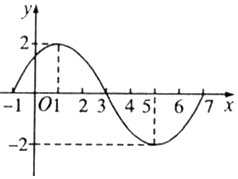 已知函数y=Asin(ωx+φ)(A>0,ω>0)在一个周期内的图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0)在一个周期内的图象如图所示.