题目内容
15.若实数x,y满足$\left\{\begin{array}{l}x-y-2≥0\\ 2x+y-2≤0\\ y+4≥0.\end{array}\right.$,则目标函数z=4x+3y的最大值为( )| A. | 0 | B. | $\frac{10}{3}$ | C. | 12 | D. | 20 |
分析 作出不等式组对应的平面区域,利用z的几何意义利用数形结合即可得到结论.
解答 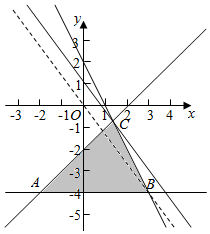 解:由约束条件作出其所确定的平面区域(阴影部分)
解:由约束条件作出其所确定的平面区域(阴影部分)
平移直线z=4x+3y,由图象可知当直线z=4x+3y经过点C时,
目标函数z=4x+3y取得最大值,
由$\left\{\begin{array}{l}{2x+y-2=0}\\{x-y-2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{4}{3}}\\{y=-\frac{2}{3}}\end{array}\right.$,
即C($\frac{4}{3}$,-$\frac{2}{3}$),
即z=4×$\frac{4}{3}$-$\frac{2}{3}$×3=$\frac{10}{3}$,
故z的最大值为$\frac{10}{3}$.
故选:B.
点评 本题主要考查线性规划的应用,利用数形结合是解决本题的关键.要求熟练掌握常见目标函数的几何意义.

练习册系列答案
相关题目
10.已知F1,F2分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,若点P是以F1F2为直径的圆与C右支的一个交点,PF1交C于另一点Q,且|PQ|=2|QF1|,则C的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
20.已知集合A={x|x2-1≥0,x∈R},B={x|0≤x<3,x∈R},则A∩B=( )
| A. | {x|1<x<3,x∈R} | B. | {x|1≤x≤3,x∈R} | C. | {x|1≤x<3,x∈R} | D. | {x|0<x<3,x∈R} |
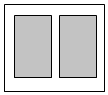 现需设计2016年春季湖北省重点高中联考协作体期中考试数学试卷,该试卷含有大小相等的左右相等两个矩形栏目(即图中阴影部分),这两栏的面积之和为720cm2,四周空白的宽度为4cm,两栏之间的中缝空白的宽度为2cm,设试卷的高和宽分别为xcm,ycm.
现需设计2016年春季湖北省重点高中联考协作体期中考试数学试卷,该试卷含有大小相等的左右相等两个矩形栏目(即图中阴影部分),这两栏的面积之和为720cm2,四周空白的宽度为4cm,两栏之间的中缝空白的宽度为2cm,设试卷的高和宽分别为xcm,ycm.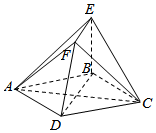 如图,四边形ABCD为菱形,EB⊥平面ABCD,EF∥BD,EF=$\frac{1}{2}$BD.
如图,四边形ABCD为菱形,EB⊥平面ABCD,EF∥BD,EF=$\frac{1}{2}$BD.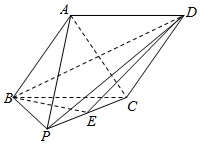 如图,在四棱锥P-ABCD中,底面ABCD是菱形,侧面PBC是直角三角形,∠PCB=90°,点E是PC的中点,且平面PBC⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,侧面PBC是直角三角形,∠PCB=90°,点E是PC的中点,且平面PBC⊥平面ABCD.