Question

1．已知函数f（x）=$\left\{\begin{array}{l}{x^3}，x≤a\\{x^2}，x＞a.\end{array}$若存在实数b，使函数g（x）=f（x）-b有两个零点，则a的取值范围是（　　）

• A． （-∞，-1）∪（0，+∞）
• B． （-∞，0）∪（1，+∞）
• C． （-∞，0）
• D． （0，1）

Answer 1

分析 由g（x）=f（x）-b有两个零点可得f（x）=b有两个零点，即y=f（x）与y=b的图象有两个交点，则函数在定义域内不能是单调函数，结合函数图象可求a的范围

解答 解：∵g（x）=f（x）-b有两个零点，
∴f（x）=b有两个零点，即y=f（x）与y=b的图象有两个交点，
由x³=x²可得，x=0或x=1
①当a＞1时，函数f（x）的图象如图所示，此时存在b，满足题意，故a＞1满足题意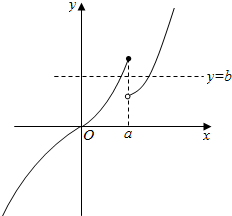

②当a=1时，由于函数f（x）在定义域R上单调递增，故不符合题意
③当0＜a＜1时，函数f（x）单调递增，故不符合题意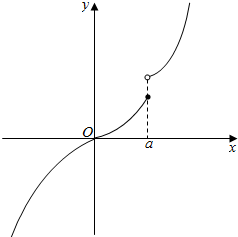

④a=0时，f（x）单调递增，故不符合题意
⑤当a＜0时，函数y=f（x）的图象如图所示，此时存在b使得，y=f（x）与y=b有两个交点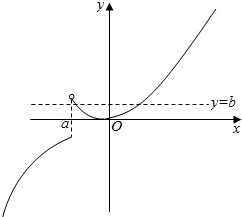

综上可得，a＜0或a＞1
则a的取值范围是（-∞，0）∪（1，+∞），
故选：B．

点评 本题考察了函数的零点问题，渗透了转化思想，数形结合、分类讨论的数学思想．