题目内容
已知函数 .
.
(Ⅰ)求证函数f(x)为奇函数;
(Ⅱ)用定义证明:函数f(x)在(1,+∞)上是增函数.
解:(Ⅰ)证明:函数的定义域是(-∞.0)∪(0,+∞)
由 ,
,
可得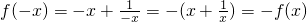 ,
,
所以函数f(x)为奇函数.
(Ⅱ)任取x1,x2∈(1,+∞),且x1<x2,
则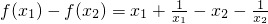 =
=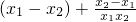 =
=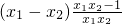 ,
,
由x1,x2∈(1,+∞),且x1<x2,可知x1<x2,x1x2-1>0,
所以f(x1)<f(x2).
即f(x1)<f(x2),
所以函数f(x)在(1,+∞)上是增函数
分析:(Ⅰ)利用奇函数的定义,考查f(-x)=-f(x)在定义域内是否恒成立,若是则为奇函数,否则不是奇函数.
(Ⅱ)利用增函数的定义,证明对于(1,+∞)内任意的x1<x2,都有f(x1)<f(x2)即可.
点评:本题考查函数奇偶性的判断、单调性的证明.严格按照定义解决.利用定义证明单调性是采用的步骤是:取值-作差-变形定号-下结论
由
 ,
,可得
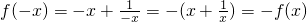 ,
,所以函数f(x)为奇函数.
(Ⅱ)任取x1,x2∈(1,+∞),且x1<x2,
则
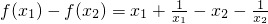 =
=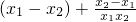 =
=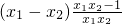 ,
,由x1,x2∈(1,+∞),且x1<x2,可知x1<x2,x1x2-1>0,
所以f(x1)<f(x2).
即f(x1)<f(x2),
所以函数f(x)在(1,+∞)上是增函数

分析:(Ⅰ)利用奇函数的定义,考查f(-x)=-f(x)在定义域内是否恒成立,若是则为奇函数,否则不是奇函数.
(Ⅱ)利用增函数的定义,证明对于(1,+∞)内任意的x1<x2,都有f(x1)<f(x2)即可.
点评:本题考查函数奇偶性的判断、单调性的证明.严格按照定义解决.利用定义证明单调性是采用的步骤是:取值-作差-变形定号-下结论

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





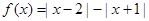 .
. ;
;
 .
. ;
; .
.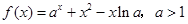 .
.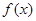 在
在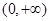 上单调递增;
上单调递增;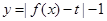 有三个零点,求
有三个零点,求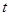 值;
值;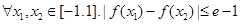 恒成立,求
恒成立,求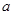 的取值范围.
的取值范围.