题目内容
(1)求sin(-
)的值;
(2)化简:
.
| 10π |
| 3 |
(2)化简:
| sin(π+α)cos(α-π)tan(3π-α) |
| sin(2π-α)cos(5π+α)tan(α-9π) |
分析:(1)原式角度变形后,利用诱导公式及特殊角的三角函数值计算即可得到结果;
(2)原式利用诱导公式变形,约分即可得到结果.
(2)原式利用诱导公式变形,约分即可得到结果.
解答:解:(1)sin(-
)=-sin
=-sin(4π-
)=sin
=sin
=
;
(2)原式=
=-1.
| 10π |
| 3 |
| 10π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| ||
| 2 |
(2)原式=
| -sinα(-cosα)(-tanα) |
| -sinα(-cosα)tanα |
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
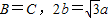 .
.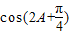 的值.
的值.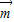 =(
=(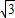 cos
cos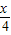 ,cos
,cos ),
),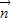 =(sin
=(sin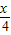 ,cos
,cos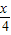 ).若
).若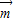 •
•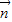 =
=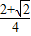 ,求sin(
,求sin(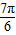 -x)的值.
-x)的值.